题目内容
直线y=2x-1与y=-x+2相交于点________,这两条直线与y轴围成的图形的面积是________.
(1,1) 
分析:让这两个函数组成方程组求得公共解即为交点坐标;这两条直线与y轴围成的图形的面积等于两条直线与y轴交点的距离为底边,以交点的横坐标为高的三角形的面积.
解答:由题意得: ,
,
解得: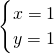 ,
,
∴直线y=2x-1与y=-x+2相交于点(1,1);
易得y=2x-1与y轴交点坐标为(0,-1),y=-x+2与y轴交点坐标为(0,2),
∴两交点之间的距离为:2-(-1)=3.
∴这两条直线与y轴围成的图形的面积是 ×3×1=
×3×1= .
.
点评:用到的知识点为:两条直线的交点坐标是这两条直线解析式组成方程组的公共解;难点是得到所求三角形面积的底边与高.

分析:让这两个函数组成方程组求得公共解即为交点坐标;这两条直线与y轴围成的图形的面积等于两条直线与y轴交点的距离为底边,以交点的横坐标为高的三角形的面积.
解答:由题意得:
 ,
,解得:
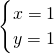 ,
,∴直线y=2x-1与y=-x+2相交于点(1,1);
易得y=2x-1与y轴交点坐标为(0,-1),y=-x+2与y轴交点坐标为(0,2),
∴两交点之间的距离为:2-(-1)=3.
∴这两条直线与y轴围成的图形的面积是
 ×3×1=
×3×1= .
.点评:用到的知识点为:两条直线的交点坐标是这两条直线解析式组成方程组的公共解;难点是得到所求三角形面积的底边与高.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2013•燕山区一模)如图,直线y=2x-1与反比例函数
(2013•燕山区一模)如图,直线y=2x-1与反比例函数 如图,直线y=kx+b经过点A(0,5),B(1,4).
如图,直线y=kx+b经过点A(0,5),B(1,4). 如图,已知直线y=2x+4与x轴交于点A,与y轴交于点B,直线AB上有一点Q在第一象限且到y轴的距离为2.
如图,已知直线y=2x+4与x轴交于点A,与y轴交于点B,直线AB上有一点Q在第一象限且到y轴的距离为2.