题目内容
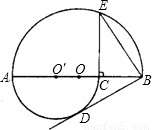
已知点O是钝角△ABC的外接圆的圆心，则钝角∠A和∠BOC之间的数量关系是________．
∠A=180°-
∠BOC
分析：首先根据题意画出图形，然后在优弧BC上取点D，连接BD，CD，由圆的内接四边形的性质与圆周角定理，即可得∠A+∠D=180°，∠BOC=2∠D，继而求得答案．
解答：
解：如图，在优弧BC上取点D，连接BD，CD，
则∠A+∠D=180°，∠BOC=2∠D，
∴∠A=180°-∠BOC．
故答案为：
点评：此题考查了圆周角定理以及圆的内接四边形的性质．此题难度不大，注意掌握数形结合思想的应用．
∠BOC分析：首先根据题意画出图形，然后在优弧BC上取点D，连接BD，CD，由圆的内接四边形的性质与圆周角定理，即可得∠A+∠D=180°，∠BOC=2∠D，继而求得答案．
解答：
解：如图，在优弧BC上取点D，连接BD，CD，则∠A+∠D=180°，∠BOC=2∠D，
∴∠A=180°-
∠BOC．故答案为：
点评：此题考查了圆周角定理以及圆的内接四边形的性质．此题难度不大，注意掌握数形结合思想的应用．
练习册系列答案
阅读快车系列答案
相关题目
