题目内容
四边形ABCD中,E,F分别是边AB,CD的中点,则AD,BC和EF的关系是
- A.AD+BC>2EF
- B.AD+BC≥2EF
- C.AD+BC<EF
- D.AD+BC≤2EF
B
分析:取AC的中点G,连接EF,EG,GF,根据三角形中位线定理求出EG= BC,GF=
BC,GF= AD,再利用三角形三边关系:两边之和大于第三边,即可得出AD,BC和EF的关系.
AD,再利用三角形三边关系:两边之和大于第三边,即可得出AD,BC和EF的关系.
解答: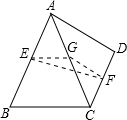 解:如图,取AC的中点G,连接EF,EG,GF,
解:如图,取AC的中点G,连接EF,EG,GF,
∵E,F分别是边AB,CD的中点,
∴EG,GF分别是△ABC和△ACD的中位线,
∴EG= BC,GF=
BC,GF= AD,
AD,
在△EGF中,由三角形三边关系得EG+GF>EF,即 BC+
BC+ AD>EF,
AD>EF,
∴AD+BC>2EF,
当AD∥BC时,点E、F、G在同一条直线上,
∴AD+BC=2EF,
所以四边形ABCD中,E,F分别是边AB,CD的中点,则AD,BC和EF的关系是AD+BC≥2EF.
故选B.
点评:此题主要考查学生对三角形中位线定理和三角形三边关系的灵活运用,要求学生应熟练掌握.
分析:取AC的中点G,连接EF,EG,GF,根据三角形中位线定理求出EG=
 BC,GF=
BC,GF= AD,再利用三角形三边关系:两边之和大于第三边,即可得出AD,BC和EF的关系.
AD,再利用三角形三边关系:两边之和大于第三边,即可得出AD,BC和EF的关系.解答:
 解:如图,取AC的中点G,连接EF,EG,GF,
解:如图,取AC的中点G,连接EF,EG,GF,∵E,F分别是边AB,CD的中点,
∴EG,GF分别是△ABC和△ACD的中位线,
∴EG=
 BC,GF=
BC,GF= AD,
AD,在△EGF中,由三角形三边关系得EG+GF>EF,即
 BC+
BC+ AD>EF,
AD>EF,∴AD+BC>2EF,
当AD∥BC时,点E、F、G在同一条直线上,
∴AD+BC=2EF,
所以四边形ABCD中,E,F分别是边AB,CD的中点,则AD,BC和EF的关系是AD+BC≥2EF.
故选B.
点评:此题主要考查学生对三角形中位线定理和三角形三边关系的灵活运用,要求学生应熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 23、如图,四边形ABCD中,对角线AC、BD相交于点E.已知:DA=DC,E为AC中点.
23、如图,四边形ABCD中,对角线AC、BD相交于点E.已知:DA=DC,E为AC中点. 如图所示,在平行四边形ABCD中,AE是∠DAB的平分线,EF∥AD交AB于点F,若AB=9,CE=4,AE=8,则DF等于( )
如图所示,在平行四边形ABCD中,AE是∠DAB的平分线,EF∥AD交AB于点F,若AB=9,CE=4,AE=8,则DF等于( ) 17、如图,在平行四边形ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交AB、CD于E、F.请写出图中三对全等的三角形:
17、如图,在平行四边形ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交AB、CD于E、F.请写出图中三对全等的三角形: 7、如图,在四边形ABCD中,AD=CB,∠ACB=∠CAD.求证:AB=CD.
7、如图,在四边形ABCD中,AD=CB,∠ACB=∠CAD.求证:AB=CD.