��Ŀ����
���и����н��ⷽ����˵����ȷ�ĸ�����
��1���û�Ԫ���ⷽ�� +
+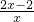 +3=0����
+3=0���� =y����ԭ���̿ɻ�Ϊy+
=y����ԭ���̿ɻ�Ϊy+ +3=0��
+3=0��
��2����x+y=a��x-y=b����2x2+2y2��ֵ�����䷽����2x2+2y2=��x+y��2+��x-y��2��
��3����x2-4x+4+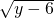 =0����x��y��ֵ���÷Ǹ����ĺ�Ϊ��⣬��ԭʽ���Ի�Ϊ��x-2��2+
=0����x��y��ֵ���÷Ǹ����ĺ�Ϊ��⣬��ԭʽ���Ի�Ϊ��x-2��2+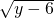
=0��
��4���ĸ�ȫ�ȵ������ı��εĵ�ש���̳�һƬ���Բ�����϶��
- A.1��
- B.2��
- C.3��
- D.4��
D
��������1����Ԫ�����ʽ���̣�Ҫ��ȷ������ʽ��y�Ĺ�ϵ��
��2���䷽����������ã�Ҫѧ����ƽ����ϵ����������֪��ϵ������
��3���䷽�����Ǹ��������ã�
��4����Ƕ���⣬Ҫ����ɵļ����Ǻ�Ϊ360�㣮
��𣺣�1���� =y����
=y����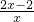 =
= ��ԭ���̿ɻ�Ϊy+
��ԭ���̿ɻ�Ϊy+ +3=0����ȷ��
+3=0����ȷ��
��2��������ȫƽ����ʽ����ȷ��
��3��Ҫ���õ�ʽ��Ϊ0��������ø�����ĺ�ƽ����Ϊ0����ȷ��
��4����Ϊ�ı��ε��ڽǺ�Ϊ360�㣬�̳�һƬ���Բ�����϶����ȷ��
��ѡD��
�����������ۺϿ�����ѧ���Ľⷽ�̵������������ı��ε����������
��������1����Ԫ�����ʽ���̣�Ҫ��ȷ������ʽ��y�Ĺ�ϵ��
��2���䷽����������ã�Ҫѧ����ƽ����ϵ����������֪��ϵ������
��3���䷽�����Ǹ��������ã�
��4����Ƕ���⣬Ҫ����ɵļ����Ǻ�Ϊ360�㣮
��𣺣�1����
 =y����
=y����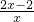 =
= ��ԭ���̿ɻ�Ϊy+
��ԭ���̿ɻ�Ϊy+ +3=0����ȷ��
+3=0����ȷ����2��������ȫƽ����ʽ����ȷ��
��3��Ҫ���õ�ʽ��Ϊ0��������ø�����ĺ�ƽ����Ϊ0����ȷ��
��4����Ϊ�ı��ε��ڽǺ�Ϊ360�㣬�̳�һƬ���Բ�����϶����ȷ��
��ѡD��
�����������ۺϿ�����ѧ���Ľⷽ�̵������������ı��ε����������

��ϰ��ϵ�д�
�����Ŀ
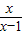 +
+ +3=0����
+3=0���� =y����ԭ���̿ɻ�Ϊy+
=y����ԭ���̿ɻ�Ϊy+ +3=0��
+3=0�� =0����x��y��ֵ���÷Ǹ����ĺ�Ϊ��⣬��ԭʽ���Ի�Ϊ��x-2��2+
=0����x��y��ֵ���÷Ǹ����ĺ�Ϊ��⣬��ԭʽ���Ի�Ϊ��x-2��2+
 +
+ +3=0����
+3=0���� =y����ԭ���̿ɻ�Ϊy+
=y����ԭ���̿ɻ�Ϊy+ +3=0��
+3=0�� =0����x��y��ֵ���÷Ǹ����ĺ�Ϊ��⣬��ԭʽ���Ի�Ϊ��x-2��2+
=0����x��y��ֵ���÷Ǹ����ĺ�Ϊ��⣬��ԭʽ���Ի�Ϊ��x-2��2+
 +
+ +3=0����
+3=0���� =y����ԭ���̿ɻ�Ϊy+
=y����ԭ���̿ɻ�Ϊy+ +3=0��
+3=0�� =0����x��y��ֵ���÷Ǹ����ĺ�Ϊ��⣬��ԭʽ���Ի�Ϊ��x-2��2+
=0����x��y��ֵ���÷Ǹ����ĺ�Ϊ��⣬��ԭʽ���Ի�Ϊ��x-2��2+