题目内容
如图,一只蚂蚁以均匀的速度沿台阶 爬行,那么蚂蚁爬行的高度
爬行,那么蚂蚁爬行的高度 随时间
随时间 变化的图象大致是( )
变化的图象大致是( )
 爬行,那么蚂蚁爬行的高度
爬行,那么蚂蚁爬行的高度 随时间
随时间 变化的图象大致是( )
变化的图象大致是( )
B
试题分析:仔细分析图形特征可得在
 段,高度
段,高度 不断增大,在
不断增大,在 段,高度
段,高度 不变,在
不变,在 段,高度
段,高度 不断增大,在
不断增大,在 段,高度
段,高度 不变,从而可以做出判断.
不变,从而可以做出判断.解:由图可得在
 段,高度
段,高度 不断增大,在
不断增大,在 段,高度
段,高度 不变,在
不变,在 段,高度
段,高度 不断增大,在
不断增大,在 段,高度
段,高度 不变,故选B.
不变,故选B.点评:实际问题的函数图象是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
 与反比例函数
与反比例函数 图象的公共点,若将一次函数
图象的公共点,若将一次函数 与
与 轴、
轴、 轴分别交于点
轴分别交于点 ,与双曲线
,与双曲线
 分别交于点
分别交于点 ,且
,且 点的坐标为
点的坐标为 .
.
 及双曲线的解析式;
及双曲线的解析式; 的坐标;
的坐标; 在什么范围内取值时,
在什么范围内取值时, >
> .
.
 交x轴于点A,交y轴于点B,BD平分∠AB0,点C是x轴的正半轴上一点,连接BC,且AC=AB.
交x轴于点A,交y轴于点B,BD平分∠AB0,点C是x轴的正半轴上一点,连接BC,且AC=AB.
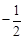

 和
和 的图象相交于A(m,3),则不等式
的图象相交于A(m,3),则不等式 的解集为
的解集为




 交于点A(-1,-5)、D(5,1),并分别与x轴、y轴交于点C、B.
交于点A(-1,-5)、D(5,1),并分别与x轴、y轴交于点C、B.