题目内容
 如图,已知?ABCD的面积是S,依次连接?ABCD各边中点构成第二个平行四边形?EFGH,再依次连接第二个平行四边形各边中点构成第三个平行四边形,…以此类推,则第2009个平行四边形的面积为
如图,已知?ABCD的面积是S,依次连接?ABCD各边中点构成第二个平行四边形?EFGH,再依次连接第二个平行四边形各边中点构成第三个平行四边形,…以此类推,则第2009个平行四边形的面积为
- A.
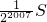
- B.
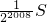
- C.
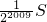
- D.无法确定
B
分析:连接EG,HF,相交于点O,有平行四边形的判定方法和平行四边形的性质:被对角线分的两个三角形的面积相等,可得新生成的平行四边形和前一个四边形的面积之间的关系,得出规律,按此规律即可求出第2009个平行四边形的面积.
解答:连接EG,HF,相交于点O,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵H和F为中点,
∴AH=BF,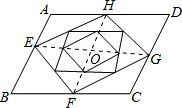
∴四边形ABFH为平行四边形,
∴AE∥HO,
同理可证:EO∥AH,
∴四边形AEOH是平行四边形,
∵EH是对角线,
∴S△AEH=S△EOH= SAEOH,
SAEOH,
同理可得:S△EOF=S△BEF= S四边形EBFO,S△CFG=S△FOG=
S四边形EBFO,S△CFG=S△FOG= S四边形FOGC,S△DHG=S△HOG=
S四边形FOGC,S△DHG=S△HOG= S四边形HOGD,
S四边形HOGD,
∴四边形EFGH的面积= 四边形ABCD的面积即为
四边形ABCD的面积即为 S,
S,
∴第三个平行四边形的面积为 ×
× S=
S= S
S
以此类推,可知每一个新生成的平行四边形都为前一个平行四边形面积的 ,
,
∴第2009个平行四边形的面积=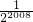 S.
S.
故选B.
点评:本题考查了平行四边形的判定和平行四边形的性质,解题的关键是找到规律,根据规律求出第2009个平行四边形的面积.
分析:连接EG,HF,相交于点O,有平行四边形的判定方法和平行四边形的性质:被对角线分的两个三角形的面积相等,可得新生成的平行四边形和前一个四边形的面积之间的关系,得出规律,按此规律即可求出第2009个平行四边形的面积.
解答:连接EG,HF,相交于点O,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵H和F为中点,
∴AH=BF,

∴四边形ABFH为平行四边形,
∴AE∥HO,
同理可证:EO∥AH,
∴四边形AEOH是平行四边形,
∵EH是对角线,
∴S△AEH=S△EOH=
 SAEOH,
SAEOH,同理可得:S△EOF=S△BEF=
 S四边形EBFO,S△CFG=S△FOG=
S四边形EBFO,S△CFG=S△FOG= S四边形FOGC,S△DHG=S△HOG=
S四边形FOGC,S△DHG=S△HOG= S四边形HOGD,
S四边形HOGD,∴四边形EFGH的面积=
 四边形ABCD的面积即为
四边形ABCD的面积即为 S,
S,∴第三个平行四边形的面积为
 ×
× S=
S= S
S以此类推,可知每一个新生成的平行四边形都为前一个平行四边形面积的
 ,
,∴第2009个平行四边形的面积=
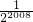 S.
S.故选B.
点评:本题考查了平行四边形的判定和平行四边形的性质,解题的关键是找到规律,根据规律求出第2009个平行四边形的面积.

练习册系列答案
相关题目
 14、如图,已知?ABCD中,AB=4,BC=6,BC边上的高AE=2,则DC边上的高AF的长是
14、如图,已知?ABCD中,AB=4,BC=6,BC边上的高AE=2,则DC边上的高AF的长是

 26、如图,已知?ABCD,AE平分∠BAD,交DC于E,DF⊥BC于F,交AE于G,且DF=AD.
26、如图,已知?ABCD,AE平分∠BAD,交DC于E,DF⊥BC于F,交AE于G,且DF=AD.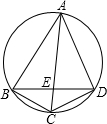 如图,已知ABCD是圆的内接四边形,对角线AC和BD相交于E,BC=CD=4,AE=6,如果线段BE和DE的长都是整数,则BD的长等于
如图,已知ABCD是圆的内接四边形,对角线AC和BD相交于E,BC=CD=4,AE=6,如果线段BE和DE的长都是整数,则BD的长等于 如图,已知ABCD是圆O的内接四边形,AB=BD,BM⊥AC于M,求证:AM=DC+CM.
如图,已知ABCD是圆O的内接四边形,AB=BD,BM⊥AC于M,求证:AM=DC+CM.