题目内容
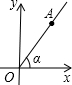如上右图，在所示的直角坐标系中，A是第一象限的点，其坐标是（3，y），且OA与x轴的正半轴的夹角α的正切值是| 4 | 3 |
分析：过点A作AB⊥x轴，根据正切等于对边比邻边列式求解即可．
解答：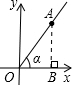
解：过点A作AB⊥x轴，
∵点A的坐标是（3，y），OA与x轴的正半轴的夹角α的正切值是
，
∴tanα=
=
，
解得y=4．
故答案为：4．
解：过点A作AB⊥x轴，∵点A的坐标是（3，y），OA与x轴的正半轴的夹角α的正切值是
| 4 |
| 3 |
∴tanα=
| y |
| 3 |
| 4 |
| 3 |
解得y=4．
故答案为：4．
点评：本题考查了锐角三角函数的定义，过点A作x轴的垂线，构造出直角三角形是利用正切列式的关键，需要熟记正切=对边：邻边．
练习册系列答案
相关题目
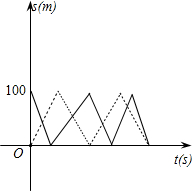
8、男、女运动员在100m直道的相对两端同时起跑，往返练习跑步，测得男运动员每百米跑12s，女运动员每百米跑15s，如上如图所示的实线和虚线分别为这两个运动员所跑路程s（m）与时间t（s）之间的函数图象，请根据图象回答：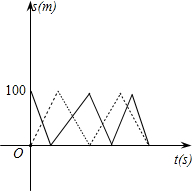
s（m）与时间t（s）之间的函数图象，请根据图象回答：