题目内容
（2013•广州）如图，在平面直角坐标系中，点O为坐标原点，点P在第一象限，⊙P与x轴交于O，A两点，点A的坐标为（6，0），⊙P的半径为| 13 |
（3，2）
（3，2）
．分析：过点P作PD⊥x轴于点D，连接OP，先由垂径定理求出OD的长，再根据勾股定理求出PD的长，故可得出答案．
解答：
解：过点P作PD⊥x轴于点D，连接OP，
∵A（6，0），PD⊥OA，
∴OD=
OA=3，
在Rt△OPD中，
∵OP=
，OD=3，
∴PD=
=
=2，
∴P（3，2）．
故答案为：（3，2）．
解：过点P作PD⊥x轴于点D，连接OP，∵A（6，0），PD⊥OA，
∴OD=
| 1 |
| 2 |
在Rt△OPD中，
∵OP=
| 13 |
∴PD=
| OP2-OD2 |
(
|
∴P（3，2）．
故答案为：（3，2）．
点评：本题考查的是垂径定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
练习册系列答案
相关题目
（2013•广州）如图所示的几何体的主视图是（ ）
（2013•广州）如图所示，四边形ABCD是梯形，AD∥BC，CA是∠BCD的平分线，且AB⊥AC，AB=4，AD=6，则tanB=（ ）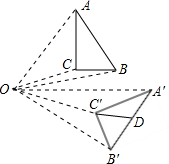
（2013•广州）如图，Rt△ABC的斜边AB=16，Rt△ABC绕点O顺时针旋转后得到Rt△A′B′C′，则Rt△A′B′C′的斜边A′B′上的中线C′D的长度为
（2013•广州）如图，在东西方向的海岸线MN上有A、B两艘船，均收到已触礁搁浅的船P的求救信号，已知船P在船A的北偏东58°方向，船P在船B的北偏西35°方向，AP的距离为30海里．
（2013•广州）如图，在平面直角坐标系中，点O为坐标原点，正方形OABC的边OA、OC分别在x轴、y轴上，点B的坐标为（2，2），反比例函数