题目内容
如图，CF平分∠DCE，点C在BD上，CE∥AB．若∠ECF=65°，则∠ABD的度数为
- A.65°
- B.110°
- C.130°
- D.135°
C
分析：根据角平分线的定义求出∠DCE，再根据两直线平行，同位角相等解答．
解答：∵CF平分∠DCE，∠ECF=65°，
∴∠DCE=2∠ECF=2×65°=130°，
∵CE∥AB，
∴∠ABD=∠DCE=130°．
故选C．
点评：本题考查了平行线的性质，角平分线的定义，是基础题，熟记性质并准确识图是解题的关键．
分析：根据角平分线的定义求出∠DCE，再根据两直线平行，同位角相等解答．
解答：∵CF平分∠DCE，∠ECF=65°，
∴∠DCE=2∠ECF=2×65°=130°，
∵CE∥AB，
∴∠ABD=∠DCE=130°．
故选C．
点评：本题考查了平行线的性质，角平分线的定义，是基础题，熟记性质并准确识图是解题的关键．
练习册系列答案
相关题目
20、（A）四边形ABCD、DEFG都是正方形，连接AE、CG．求证：AE=CG；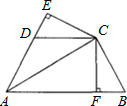
如图，AC平分∠EAB，DC=BC，CE⊥AD，交AD的延长线于点E，CF⊥AB，垂足为F．试说明：DE=BF．
已知：如图，AC平分∠BAD，CE⊥AB于E CF⊥AD于F，且BC=DC．求证：BE=DF．
（A）四边形ABCD、DEFG都是正方形，连接AE、CG．求证：AE=CG；