题目内容
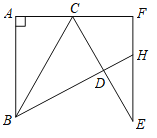
【题目】如图，将ΔABC沿BC翻折得到ΔDBC，再将ΔDBC绕C点逆时针旋转60°得到ΔFEC，延长B D交EF于H，已知∠ABC＝30°，∠BAC＝90°，AC＝1，则四边形CDHF的面积为（ ）
A. 
B. 
C. 
D. ．
【答案】C
【解析】
解：∵∠ABC=30°，∠BAC=90°，AC=1，∴BC=2AC=2，∴AB=
=
由翻折、旋转的性质知：AC=CD=CF=1，∠ACB=∠BCD=∠FCE=60°，∴∠ACF=180°，即点A、C、F三点共线，CE=CB=2，EF=BD=AB=
，∠E=∠ABC=30°，∴DE=2﹣1=1．在Rt△DEH中，DH=
DE=，S四边形CDHF=S△CEF﹣S△DEH=
×1×﹣×1×=．故选C．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
【题目】高尔夫运动员将一个小球沿与地面成一定角度的方向击出，在不考虑空气阻力的条件下，小球的飞行高度h（m）与它的飞行时间（s）满足二次函数关系，t与h的几组对应值如下表所示：
t（s） | 0 | 0.5 | 1 | 1.5 | 2 | … |
h（m） | 0 | 8.75 | 15 | 18.75 | 20 | … |
（1）求h与t之间的函数关系式（不要求写t的取值范围）；
（2）求小球飞行3s时的高度．
