题目内容
14.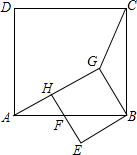 如图,在Rt△AGB中,∠AGB=90°,∠GAB=30°,以GB为边在GB的下方作正方形GBEH,以AB为边在AB的上方作正方形ABCD,连结CG.若FB=2,则CG2的值为15-6$\sqrt{3}$.
如图,在Rt△AGB中,∠AGB=90°,∠GAB=30°,以GB为边在GB的下方作正方形GBEH,以AB为边在AB的上方作正方形ABCD,连结CG.若FB=2,则CG2的值为15-6$\sqrt{3}$.
分析 作GM⊥BC于M,由四边形ABCD是正方形可以得出AB=BC,∠ABC=90°,由∠AGB=90°,∠GAB=30°,可以得出∠GBA=60°,从而得到∠EBF=30°,∠GBM=30°,由FB得到BE=GB=$\sqrt{3}$,可以求出GM=$\frac{\sqrt{3}}{2}$,BM=$\frac{3}{2}$,可以求出CM=2$\sqrt{3}$-$\frac{3}{2}$,在Rt△GMC中,由勾股定理就可以求出CG2的值.
解答 解:作GM⊥BC于M,
∴∠GMC=∠GMB=90°.
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°.
∵∠AGB=90°,∠GAB=30°,
∴∠GBA=60°,AB=2GB
∴∠EBF=30°,∠GBM=30°,
∵FB=2,
∴BE=GB=$\sqrt{3}$,
∴AB=BC=2$\sqrt{3}$,GM=$\frac{1}{2}$GB=$\frac{\sqrt{3}}{2}$,BM=$\frac{3}{2}$,
∴CM=2$\sqrt{3}$-$\frac{3}{2}$,
在Rt△GMC中,由勾股定理,得
CG2=GM2+MC2
=($\frac{\sqrt{3}}{2}$)2+(2$\sqrt{3}$-$\frac{3}{2}$)2
=15-6$\sqrt{3}$.
故答案为:15-6$\sqrt{3}$.
点评 本题考查了正方形的性质,含30度角的直角三角形的性质,勾股定理的运用.在解答中制造直角三角形运用勾股定理是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
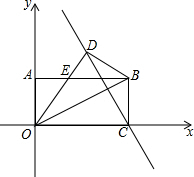 如图,矩形OABC在平面直角坐标系中,OA=2,∠BOC=30°,把△OBC沿OB对折,点C落在点D处,线段OD与AB交于点E.若点P在直线CD上,并且△OEP为直角三角形,求P点坐标.
如图,矩形OABC在平面直角坐标系中,OA=2,∠BOC=30°,把△OBC沿OB对折,点C落在点D处,线段OD与AB交于点E.若点P在直线CD上,并且△OEP为直角三角形,求P点坐标.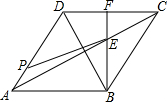 已知菱形ABCD边长为5cm,tan∠DAB=$\frac{4}{3}$,连接AC、BD,过点B作BE⊥AB分别交AC、CD于E、F.若点P为AD上一点,且∠DPE+∠DAB=90°,则AP长为$\frac{5}{3}$.
已知菱形ABCD边长为5cm,tan∠DAB=$\frac{4}{3}$,连接AC、BD,过点B作BE⊥AB分别交AC、CD于E、F.若点P为AD上一点,且∠DPE+∠DAB=90°,则AP长为$\frac{5}{3}$.
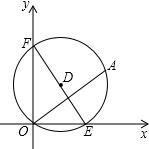 如图,在平面直角坐标系中,点A的坐标是(4,3),动圆D经过A、O,分别与两坐标轴的正半轴交于点E、F.当EF⊥OA时,此时EF=$\frac{125}{24}$.
如图,在平面直角坐标系中,点A的坐标是(4,3),动圆D经过A、O,分别与两坐标轴的正半轴交于点E、F.当EF⊥OA时,此时EF=$\frac{125}{24}$.
 如图,⊙O的半径为10cm,G是直径AB上一点,弦CD经过点G,CD=16cm,AE⊥CD于E,BF⊥CD于F,求AE-BF的值.
如图,⊙O的半径为10cm,G是直径AB上一点,弦CD经过点G,CD=16cm,AE⊥CD于E,BF⊥CD于F,求AE-BF的值.