题目内容
设直线 (n为自然数)与两坐标轴围成的三角形面积为Sn(n=1,2,…2000),则S1+S2+…+S2000的值为
(n为自然数)与两坐标轴围成的三角形面积为Sn(n=1,2,…2000),则S1+S2+…+S2000的值为
- A.1
- B.

- C.

- D.

C
分析:先求出直线与坐标轴的两交点坐标分别为(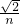 ,0),(0,
,0),(0,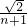 );然后计算Sn=
);然后计算Sn= •
•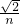
 =
= =
= -
- ,再分别计算S1,S2…S2000,最后把它们相加即可.
,再分别计算S1,S2…S2000,最后把它们相加即可.
解答:令y=0,则x=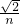 ;令x=0,则y=
;令x=0,则y=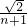 ;所以直线与坐标轴的两交点坐标分别为(
;所以直线与坐标轴的两交点坐标分别为(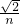 ,0),(0,
,0),(0,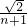 ).
).
所以Sn= •
•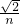
 =
= =
= -
- ,(n为自然数),
,(n为自然数),
当n=1,S1= -
- ;
;
当n=2,S2= -
- ;
;
…
当n=2000,S2000= -
-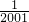 ;
;
则S1+S2+…+S2000= -
- +
+
 …+
…+ -
-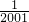 =1-
=1-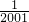 =
= .
.
故选C.
点评:本题考查了一次函数y=kx+b(k≠0,k,b为常数)与坐标轴所围成的三角形的面积计算.要学会计算一次函数与坐标轴的交点坐标.同时考查了运用 =
= -
- (n为自然数)进行计算的方法.
(n为自然数)进行计算的方法.
分析:先求出直线与坐标轴的两交点坐标分别为(
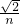 ,0),(0,
,0),(0,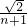 );然后计算Sn=
);然后计算Sn= •
•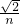
 =
= =
= -
- ,再分别计算S1,S2…S2000,最后把它们相加即可.
,再分别计算S1,S2…S2000,最后把它们相加即可.解答:令y=0,则x=
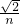 ;令x=0,则y=
;令x=0,则y=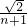 ;所以直线与坐标轴的两交点坐标分别为(
;所以直线与坐标轴的两交点坐标分别为(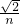 ,0),(0,
,0),(0,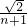 ).
).所以Sn=
 •
•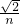
 =
= =
= -
- ,(n为自然数),
,(n为自然数),当n=1,S1=
 -
- ;
;当n=2,S2=
 -
- ;
;…
当n=2000,S2000=
 -
-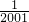 ;
;则S1+S2+…+S2000=
 -
- +
+
 …+
…+ -
-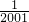 =1-
=1-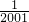 =
= .
.故选C.
点评:本题考查了一次函数y=kx+b(k≠0,k,b为常数)与坐标轴所围成的三角形的面积计算.要学会计算一次函数与坐标轴的交点坐标.同时考查了运用
 =
= -
- (n为自然数)进行计算的方法.
(n为自然数)进行计算的方法. 
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (n为自然数)与两坐标轴围成的三角形面积为
(n为自然数)与两坐标轴围成的三角形面积为 (n=1、2、…、2005),则
(n=1、2、…、2005),则 的值为( )
的值为( ) B
B  C
C  D
D 
 (n为自然数)与两坐标轴围成的三角形面积为
(n为自然数)与两坐标轴围成的三角形面积为 (n=1、2、…、2005),则
(n=1、2、…、2005),则 的值为( )
的值为( ) B
B  C
C
 D
D

 (n为自然数)与两坐标轴围成的三角形面积为Sn(n=1,2,…2000),则S1+S2+…+S2000的值为( )
(n为自然数)与两坐标轴围成的三角形面积为Sn(n=1,2,…2000),则S1+S2+…+S2000的值为( )


 (n为自然数)与两坐标轴围成的三角形面积为
(n为自然数)与两坐标轴围成的三角形面积为 (n=1、2、…、2005),则
(n=1、2、…、2005),则 的值为
的值为



 (n为自然数)与两坐标轴围成的三角形面积为
(n为自然数)与两坐标轴围成的三角形面积为 (n=1、2、…、2005),则
(n=1、2、…、2005),则 的值为( )
的值为( ) B
B  C
C  D
D 