题目内容
 11、如图,已知AB=AD,∠B=∠D,在求证BC=DC的过程中,正确添加一条辅助线的方法是:连接
11、如图,已知AB=AD,∠B=∠D,在求证BC=DC的过程中,正确添加一条辅助线的方法是:连接BD
.分析:作辅助线连接BD,构建等腰△ABD.在△ABD中,根据等腰三角形的性质知两个底角∠ADB=∠ABD,再根据已知条件∠B=∠D,从而求得∠CBD=∠CDB,易证明CB=CD(等角对等边).
解答: 证明:连接BD(如图),
证明:连接BD(如图),
∵AB=AD,
∴∠ADB=∠ABD(等边对等角),
又∵∠B=∠D,
∴∠B-∠ABD=∠D-∠ADB,
即∠CBD=∠CDB,
∴CB=CD(等角对等边).
故答案为:BD.
 证明:连接BD(如图),
证明:连接BD(如图),∵AB=AD,
∴∠ADB=∠ABD(等边对等角),
又∵∠B=∠D,
∴∠B-∠ABD=∠D-∠ADB,
即∠CBD=∠CDB,
∴CB=CD(等角对等边).
故答案为:BD.
点评:本题考查了全等三角形的判定与性质.解答时,借助于辅助线BD将隐含在题中的条件“△ABD是等腰三角形”给挖掘了出来,给证明∠CBD=∠CDB提供了有力的依据.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
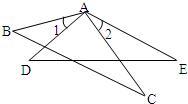 16、如图,已知AB=AD,∠1=∠2,要使△ABC≌△ADE,还需添加的条件是(只需填一个)
16、如图,已知AB=AD,∠1=∠2,要使△ABC≌△ADE,还需添加的条件是(只需填一个) 如图,已知AB⊥AD,CD⊥AD,垂足分别为A、D,AD=6,AB=5,CD=3,P是线段AD上的一个动点,设AP=x,DP=y,
如图,已知AB⊥AD,CD⊥AD,垂足分别为A、D,AD=6,AB=5,CD=3,P是线段AD上的一个动点,设AP=x,DP=y, 25、如图,已知AB=AD,AC=AE,∠1=∠2,求证△ABC≌△ADE.
25、如图,已知AB=AD,AC=AE,∠1=∠2,求证△ABC≌△ADE. 27、如图,已知AB=AD,BC=DC,BD交AC于点O,请分别说明下列判断成立的理由:
27、如图,已知AB=AD,BC=DC,BD交AC于点O,请分别说明下列判断成立的理由: 如图,已知AB=AD,点E、F分别是CD、BC的中点,BF=CE,求证:AE=AF.
如图,已知AB=AD,点E、F分别是CD、BC的中点,BF=CE,求证:AE=AF.