题目内容
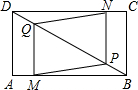 (2013•仓山区模拟)如图,四边形ABCD为矩形,AB=4,BC=3,动点M、N分别从点A、C同时出发,以每秒1个单位的速度运动,其中点M沿AB向终点B运动,点N沿CD向终点D运动,过点N做NP⊥CD于点N,交BD于P,过点M作MQ⊥AB,交BD于点Q,连接NQ、MP,当两点运动了t秒时
(2013•仓山区模拟)如图,四边形ABCD为矩形,AB=4,BC=3,动点M、N分别从点A、C同时出发,以每秒1个单位的速度运动,其中点M沿AB向终点B运动,点N沿CD向终点D运动,过点N做NP⊥CD于点N,交BD于P,过点M作MQ⊥AB,交BD于点Q,连接NQ、MP,当两点运动了t秒时(1)若t=1,即AM=CN=1时,求证:四边形MPNQ是平行四边形;
(2)若四边形MPNQ是菱形,求t的值;
(3)设四边形MPNQ的面积为S,求S关于t的函数解析式;并回答:当t为何值时,y随x的增大而减小.
分析:(1)先由矩形的性质及已知条件得出∠ABD=∠CDB,BM=DN,再利用ASA证明△BMQ≌△DNP,根据全等三角形的性质及平行线的判定得到MQ=NP,MQ∥NP,从而证明出四边形MPNQ是平行四边形;
(2)如图1,延长NP交AB于E,由tan∠DBA=
=
=
,即
=
=
,得出PE=
t,QM=
(4-t),再根据菱形的性质得出QM=MP,由此列出方程[
(4-t)]2=(
t)2+(4-2t)2,解方程即可;
(3)由于0≤t≤4且t≠2,所以分两种情况进行讨论:①0≤t<2;②2<t≤4.先用含t的代数式分别表示QM,ME,再根据平行四边形的面积=底×高得到S关于t的函数解析式,然后根据二次函数的增减性即可得出t为何值时,y随x的增大而减小.
(2)如图1,延长NP交AB于E,由tan∠DBA=
| PE |
| BE |
| QM |
| BM |
| DA |
| AB |
| PE |
| t |
| QM |
| 4-t |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
(3)由于0≤t≤4且t≠2,所以分两种情况进行讨论:①0≤t<2;②2<t≤4.先用含t的代数式分别表示QM,ME,再根据平行四边形的面积=底×高得到S关于t的函数解析式,然后根据二次函数的增减性即可得出t为何值时,y随x的增大而减小.
解答:解:(1)∵四边形ABCD为矩形,
∴AB=CD,AB∥CD,
∴∠ABD=∠CDB.
∵AM=CN,
∴AB-AM=CD-CN,即BM=DN.
在△BMQ与△DNP中,
,
∴△BMQ≌△DNP(ASA),
∴MQ=NP,∠MQB=∠NPD,
∴MQ∥NP,
∴四边形MPNQ是平行四边形;
(2)如图1,延长NP交AB于E,则NE⊥AB,四边形BENC为矩形,
∵AM=CN=BE=1•t=t,
∴BM=AB-AM=4-t,ME=|BM-BE|=|4-t-t|=|4-2t|,
∵tan∠DBA=
=
=
,
∴
=
=
,
∴PE=
t,QM=
(4-t),
 若四边形MPNQ是菱形,则QM=MP,
若四边形MPNQ是菱形,则QM=MP,
∴[
(4-t)]2=(
t)2+(4-2t)2,
整理,得8t2-23t+14=0,
解得t=2或
,
∵t=2时,M、N分别在AB、CD的中点,即此时M、Q、P、N四点共线,
∴t=2不合题意,舍去,即t=
.
故四边形MPNQ是菱形时,t的值为
;
(3)分两种情况:
①当0≤t<2时,如图1,
∵QM=
(4-t),ME=BM-BE=4-t-t=4-2t,
∴平行四边形MPNQ的面积S=QM•ME,
=
(4-t)•(4-2t)
=
t2-9t+12
=
(t2-6t)+12
=
(t-3)2-
,
∴当0≤t<2时,y随x的增大而减小;
 ②当2<t≤4时,如图2,
②当2<t≤4时,如图2,
∵QM=
(4-t),ME=BE-BM=t-(4-t)=2t-4,
∴平行四边形MPNQ的面积S=QM•ME,
=
(4-t)•(2t-4)
=-
t2+9t-12
=-
(t2-6t)-12
=-
(t-3)2+
,
∴当3<t≤4时,y随x的增大而减小.
综上所述,S关于t的函数解析式为S=
,且当0≤t<2或3<t≤4时,y随x的增大而减小.
∴AB=CD,AB∥CD,
∴∠ABD=∠CDB.
∵AM=CN,
∴AB-AM=CD-CN,即BM=DN.
在△BMQ与△DNP中,
|
∴△BMQ≌△DNP(ASA),
∴MQ=NP,∠MQB=∠NPD,
∴MQ∥NP,
∴四边形MPNQ是平行四边形;
(2)如图1,延长NP交AB于E,则NE⊥AB,四边形BENC为矩形,
∵AM=CN=BE=1•t=t,
∴BM=AB-AM=4-t,ME=|BM-BE|=|4-t-t|=|4-2t|,
∵tan∠DBA=
| PE |
| BE |
| QM |
| BM |
| DA |
| AB |
∴
| PE |
| t |
| QM |
| 4-t |
| 3 |
| 4 |
∴PE=
| 3 |
| 4 |
| 3 |
| 4 |
 若四边形MPNQ是菱形,则QM=MP,
若四边形MPNQ是菱形,则QM=MP,∴[
| 3 |
| 4 |
| 3 |
| 4 |
整理,得8t2-23t+14=0,
解得t=2或
| 7 |
| 8 |
∵t=2时,M、N分别在AB、CD的中点,即此时M、Q、P、N四点共线,
∴t=2不合题意,舍去,即t=
| 7 |
| 8 |
故四边形MPNQ是菱形时,t的值为
| 7 |
| 8 |
(3)分两种情况:
①当0≤t<2时,如图1,
∵QM=
| 3 |
| 4 |
∴平行四边形MPNQ的面积S=QM•ME,
=
| 3 |
| 4 |
=
| 3 |
| 2 |
=
| 3 |
| 2 |
=
| 3 |
| 2 |
| 3 |
| 2 |
∴当0≤t<2时,y随x的增大而减小;
 ②当2<t≤4时,如图2,
②当2<t≤4时,如图2,∵QM=
| 3 |
| 4 |
∴平行四边形MPNQ的面积S=QM•ME,
=
| 3 |
| 4 |
=-
| 3 |
| 2 |
=-
| 3 |
| 2 |
=-
| 3 |
| 2 |
| 3 |
| 2 |
∴当3<t≤4时,y随x的增大而减小.
综上所述,S关于t的函数解析式为S=
|
点评:本题是四边形综合题,考查了矩形的性质,平行线、全等三角形的判定与性质,平行四边形的判定,三角函数的定义,菱形的性质,平行四边形的面积,二次函数的性质,综合性较强,难度适中.运用数形结合、分类讨论是解题的关键.

练习册系列答案
相关题目
 (2013•仓山区模拟)如图,a∥b,∠1=30°,则∠2的度数是( )
(2013•仓山区模拟)如图,a∥b,∠1=30°,则∠2的度数是( ) (2013•仓山区模拟)如图,⊙M与x轴相切与原点,平行于y轴的直线交⊙M于P、Q两点,P点在Q点的下方,若点P的坐标是
(2013•仓山区模拟)如图,⊙M与x轴相切与原点,平行于y轴的直线交⊙M于P、Q两点,P点在Q点的下方,若点P的坐标是 (2013•仓山区模拟)如图,已知抛物线y=ax2+bx+c的顶点坐标是C(2,-1),与x轴交于点A(1,0),其对称轴与x轴相交于点F.
(2013•仓山区模拟)如图,已知抛物线y=ax2+bx+c的顶点坐标是C(2,-1),与x轴交于点A(1,0),其对称轴与x轴相交于点F.