题目内容
在△ABC中,AD是BC上的高,且AD= BC,E,F分别是AB,AC的中点,以EF为直径的圆与BC的位置关系是
BC,E,F分别是AB,AC的中点,以EF为直径的圆与BC的位置关系是
- A.相离
- B.相切
- C.相交
- D.相切或相交
B
分析:如图先根据中位线定理得到EF∥BC,EF= BC,再结合条件求出以EF为直径的圆的圆心到直线BC的距离等于OD(平行线间的距离处处相等),从而根据直线和圆的位置关系可知以EF为直径的圆与BC的位置关系是相切.
BC,再结合条件求出以EF为直径的圆的圆心到直线BC的距离等于OD(平行线间的距离处处相等),从而根据直线和圆的位置关系可知以EF为直径的圆与BC的位置关系是相切.
解答: 解:如图,
解:如图,
∵E,F分别是AB,AC的中点,
∴EF∥BC,EF= BC,
BC,
∵AD是BC上的高,且AD= BC,
BC,
∴EF=AD,
∴OD=OA= AD=
AD= EF;
EF;
所以以EF为直径的圆的圆心到直线BC的距离等于OD
即以EF为直径的圆与BC的位置关系是相切.
故选B.
点评:直线和圆的位置关系的确定一般是利用圆心到直线的距离与半径比较来判断.若圆心到直线的距离是d,半径是r,则①d>r,直线和圆相离,没有交点;②d=r,直线和圆相切,有一个交点;③d<r,直线和圆相交,有两个交点.本题还要结合中位线定理和平行线间的距离处处相等来进行判断.
分析:如图先根据中位线定理得到EF∥BC,EF=
 BC,再结合条件求出以EF为直径的圆的圆心到直线BC的距离等于OD(平行线间的距离处处相等),从而根据直线和圆的位置关系可知以EF为直径的圆与BC的位置关系是相切.
BC,再结合条件求出以EF为直径的圆的圆心到直线BC的距离等于OD(平行线间的距离处处相等),从而根据直线和圆的位置关系可知以EF为直径的圆与BC的位置关系是相切.解答:
 解:如图,
解:如图,∵E,F分别是AB,AC的中点,
∴EF∥BC,EF=
 BC,
BC,∵AD是BC上的高,且AD=
 BC,
BC,∴EF=AD,
∴OD=OA=
 AD=
AD= EF;
EF;所以以EF为直径的圆的圆心到直线BC的距离等于OD
即以EF为直径的圆与BC的位置关系是相切.
故选B.
点评:直线和圆的位置关系的确定一般是利用圆心到直线的距离与半径比较来判断.若圆心到直线的距离是d,半径是r,则①d>r,直线和圆相离,没有交点;②d=r,直线和圆相切,有一个交点;③d<r,直线和圆相交,有两个交点.本题还要结合中位线定理和平行线间的距离处处相等来进行判断.

练习册系列答案
相关题目
 在△ABC中,AD是高,矩形PQMN的顶点P、N分别在AB、AC上,QM在边BC上.若BC=8cm,AD=6cm,且PN=2PQ,求矩形PQMN的周长.
在△ABC中,AD是高,矩形PQMN的顶点P、N分别在AB、AC上,QM在边BC上.若BC=8cm,AD=6cm,且PN=2PQ,求矩形PQMN的周长.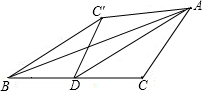 如图,在△ABC中,AD是BC上的中线,BC=4,∠ADC=30°,把△ADC沿AD所在直线翻折后点C落在点C′的位置,那么点D到直线BC′的距离是
如图,在△ABC中,AD是BC上的中线,BC=4,∠ADC=30°,把△ADC沿AD所在直线翻折后点C落在点C′的位置,那么点D到直线BC′的距离是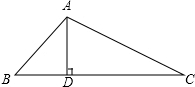
 (2013•温州二模)如图,在△ABC中,AD是它的角平分线,∠C=90°,E在AB边上,以AE为直径的⊙O交BC于点D,交AC于点F.
(2013•温州二模)如图,在△ABC中,AD是它的角平分线,∠C=90°,E在AB边上,以AE为直径的⊙O交BC于点D,交AC于点F. 如图,在△ABC中,AD是∠BAC的平分线,DE、DF分别是△ABD和△ACD的高线,求证:AD⊥EF.
如图,在△ABC中,AD是∠BAC的平分线,DE、DF分别是△ABD和△ACD的高线,求证:AD⊥EF.