题目内容
如图所示的方格纸中，有△ABC和半径为2的⊙P，点A、B、C、P均在格点上（每个小方格的顶点叫格点）．每个小方格都是边长为1的正方形，将△ABC沿水平方向向左平移________单位时，⊙P与直线AC相切．
5-
或5+
分析：平移后利用切线的性质作PD⊥A′C′于点D求得PD，再求得PA′的长，进而得出PA-PA′和AA″的长，即可求得平移的距离．
解答：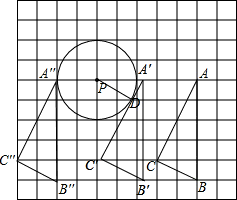
解：∵A′C′与⊙P相切，
作PD⊥A′C′于点D，
∵半径为2，
∴PD=2，
∵每个小方格都是边长为1的正方形，
∴AB=5，AC=2，
∴cosA=
=
，
∴PA′=PD÷cosA=2÷=，
∴AA′=5-，AA″=5+，
故答案为5-或5+．
点评：本题考查了切线的性质及勾股定理的相关知识，考查的知识点比较多，题目难度不太大．
或5+分析：平移后利用切线的性质作PD⊥A′C′于点D求得PD，再求得PA′的长，进而得出PA-PA′和AA″的长，即可求得平移的距离．
解答：
解：∵A′C′与⊙P相切，作PD⊥A′C′于点D，
∵半径为2，
∴PD=2，
∵每个小方格都是边长为1的正方形，
∴AB=5，AC=2
，∴cosA=
=，∴PA′=PD÷cosA=2÷
=，∴AA′=5-
，AA″=5+，故答案为5-
或5+．点评：本题考查了切线的性质及勾股定理的相关知识，考查的知识点比较多，题目难度不太大．
练习册系列答案
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案
相关题目
18、以如图所示的方格纸中，每个小正方形的边长为1，如果以MN所在的直线为y轴，以小正方形的边长为单位长度建立平面直角坐标系，使A点与B点关于原点对称，则这时C点的坐标可能是（ ）
26、在如图所示的方格纸中，经过线段AB外一点C，D，不用量角器与三角尺，仅用直尺，分别画线段AB的垂线和平行线，并用符号表示出来．
如图所示的方格纸中，各小正方形的边长均为1．
如图所示的方格纸中的小正方形的边长都是1，△ABC的顶点坐标为A（0，-2），B（3，-1），C（2，1），请画出△ABC关于y轴对称的图形△A1B1C1并直接写出B1、C1点的坐标．