题目内容
（1998•绍兴）已知：如图，面积为2的四边形ABCD内接于⊙O，对角线AC经过圆心，若∠BAD=45°，CD=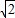
，则AB的长等于 ．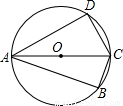
【答案】分析：延长BC、AD交于点E．可得等腰直角三角形ABE和等腰直角三角形DEC，设AB为x，则BC=x-2，CE=2，DE=
，AD=
x-
，由四边形ABCD面积为2得
×
（
x-
）+
x（x-2）=2，解得x=
，即求AB的长．
解答：
解：延长BC、AD交于点E．
∵∠BAD=45°，
∴△ABE和△DEC是等腰直角三角形．
∵CD=
，
设AB为x，
则BC=x-2，CE=2，DE=
，AD=
x-
．
∵四边形ABCD面积为2，
∴
×
（
x-
）+
x（x-2）=2，
解得x=
．
即AB=
．
点评：把有一个直角的四边形添加辅助线转化成直角三角形来解．
，AD=x-，由四边形ABCD面积为2得×（x-）+x（x-2）=2，解得x=，即求AB的长．解答：
解：延长BC、AD交于点E．∵∠BAD=45°，
∴△ABE和△DEC是等腰直角三角形．
∵CD=
，设AB为x，
则BC=x-2，CE=2，DE=
，AD=x-．∵四边形ABCD面积为2，
∴
×（x-）+x（x-2）=2，解得x=
．即AB=
．点评：把有一个直角的四边形添加辅助线转化成直角三角形来解．
练习册系列答案
学习实践园地系列答案
相关题目
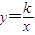上有两点A（x1，y1）、B（x2，y2），若x2＜x1＜0，则y1与y2的大小关系是（ ）