题目内容
在菱形ABCD和菱形A′B′C′D′中,∠A=∠A′=60°,若AB:A′B′=1: ,则BD:A′C′=________.
,则BD:A′C′=________.
1:3
分析:利用菱形的性质以及等边三角形的判定与性质得出BD,A′C′的长,进而得出BD:A′C′的值.
解答: 解:连接B′D′.
解:连接B′D′.
∵在菱形ABCD和菱形A′B′C′D′中,∠A=∠A′=60°,
∴AB=AD,A′B′=A′D′,
∴△ABD是等边三角形,△A′B′D′是等边三角形,
∴∠D′A′0=∠OA′B′=30°,
∵AB:A′B′=1: ,
,
∴设AB=1,A′B′= ,
,
∴AD=AB=BD=1,
∴A′O=A′D′cos30°= ×
× =
= ,
,
∴A′C′=2× =3,
=3,
则BD:A′C′=1:3.
故答案为:1:3.
点评:此题主要考查了菱形的性质和等边三角性质和判定等知识,根据已知得出A′C′的长是解题关键.
分析:利用菱形的性质以及等边三角形的判定与性质得出BD,A′C′的长,进而得出BD:A′C′的值.
解答:
 解:连接B′D′.
解:连接B′D′.∵在菱形ABCD和菱形A′B′C′D′中,∠A=∠A′=60°,
∴AB=AD,A′B′=A′D′,
∴△ABD是等边三角形,△A′B′D′是等边三角形,
∴∠D′A′0=∠OA′B′=30°,
∵AB:A′B′=1:
 ,
,∴设AB=1,A′B′=
 ,
,∴AD=AB=BD=1,
∴A′O=A′D′cos30°=
 ×
× =
= ,
,∴A′C′=2×
 =3,
=3,则BD:A′C′=1:3.
故答案为:1:3.
点评:此题主要考查了菱形的性质和等边三角性质和判定等知识,根据已知得出A′C′的长是解题关键.

练习册系列答案
相关题目
 如图,在菱形ABCD和菱形BEFG中,点A、B、E在同一直线上,P是线段DF的中点,连接PG,PC.若∠ABC=∠BEF=60°,则
如图,在菱形ABCD和菱形BEFG中,点A、B、E在同一直线上,P是线段DF的中点,连接PG,PC.若∠ABC=∠BEF=60°,则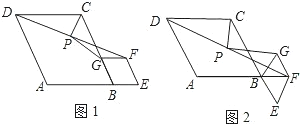 原问题中的其他条件不变,请你直接写出
原问题中的其他条件不变,请你直接写出

