题目内容
如图所示，已知矩形AECF∽矩形BECD，且AF=FD，那么AE与AF的比值是
- A.
- B.
- C.
- D.
C
分析：根据相似多边形的性质：对应边成比例，列方程解答．
解答：设AF=FD=y，DC=x，根据题意得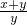
=
，
整理得-
-1=0，
设=t，
原方程可化为：t-
-1=0，
即t2-t-1=0，
解得t=
（负值舍去）或t=．
由于两四边形相似，所以AE与AF的比值是=t=（1+
）：2．
故选C．
点评：本题考查相似多边形的性质．相似多边形对应边之比、周长之比等于相似比．这种长宽比为（1+）：2的四边形被称为黄金四边形，在古希腊的建筑中很常见，给人以和谐庄重的感觉．
分析：根据相似多边形的性质：对应边成比例，列方程解答．
解答：设AF=FD=y，DC=x，根据题意得
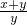=，整理得
--1=0，设
=t，原方程可化为：t-
-1=0，即t2-t-1=0，
解得t=
（负值舍去）或t=．由于两四边形相似，所以AE与AF的比值是
=t=（1+）：2．故选C．
点评：本题考查相似多边形的性质．相似多边形对应边之比、周长之比等于相似比．这种长宽比为（1+
）：2的四边形被称为黄金四边形，在古希腊的建筑中很常见，给人以和谐庄重的感觉． 
练习册系列答案
单元期中期末卷系列答案
相关题目
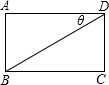如图所示，已知矩形ABCD（AD＞AB）中，AB=a，∠BDA=θ，试用a与θ表示：AD=
如图所示，已知矩形ABCD的边AB=3cm，AD=4cm．
如图所示，已知矩形ABCD中两条对角线AC、BD相交于点O，∠ADB=30°，DF∥AC交BC的延长线于F点，