题目内容
 如图,等腰△ABC中,AB=AC,P为其底角平分线的交点,将△BCP沿CP折叠,使B点恰好落在AC边上的点D处,若DA=DP,则∠A的度数为
如图,等腰△ABC中,AB=AC,P为其底角平分线的交点,将△BCP沿CP折叠,使B点恰好落在AC边上的点D处,若DA=DP,则∠A的度数为
- A.20°
- B.30°
- C.32°
- D.36°
D
分析:由题意可得点P是△ABC的内心,连接AP,则AP平分∠BAC,设∠A=2x,分别表示出∠PBC,∠PCD,在△APD中利用三角形的内角和为180°,可得出x的值,继而得出答案.
解答:连接AP,

∵P为其底角平分线的交点,
∴点P是△ABC的内心,
∴AP平分∠BAC,
∵AB=AC,
∴∠ABC=∠ACB,
设∠A=2x,则∠DAP=x,∠PBC=∠PCB=45°- x,
x,
∵DA=DP,
∴∠DAP=∠DPA,
由折叠的性质可得:∠PDC=∠PBC=45°- x,
x,
则∠ADP=180°-∠PDC=135°+ x,
x,
在△ADP中,∠DAP+∠DPA+∠ADP=180°,即x+x+135°+ x=180°,
x=180°,
解得:x=18,
则∠A=2x=36°.
故选D.
点评:本题考查了翻折变换的知识,解答本题的关键是判断出点P是三角形的内心,注意熟练掌握三角形的内角和定理,难度一般.
分析:由题意可得点P是△ABC的内心,连接AP,则AP平分∠BAC,设∠A=2x,分别表示出∠PBC,∠PCD,在△APD中利用三角形的内角和为180°,可得出x的值,继而得出答案.
解答:连接AP,

∵P为其底角平分线的交点,
∴点P是△ABC的内心,
∴AP平分∠BAC,
∵AB=AC,
∴∠ABC=∠ACB,
设∠A=2x,则∠DAP=x,∠PBC=∠PCB=45°-
 x,
x,∵DA=DP,
∴∠DAP=∠DPA,
由折叠的性质可得:∠PDC=∠PBC=45°-
 x,
x,则∠ADP=180°-∠PDC=135°+
 x,
x,在△ADP中,∠DAP+∠DPA+∠ADP=180°,即x+x+135°+
 x=180°,
x=180°,解得:x=18,
则∠A=2x=36°.
故选D.
点评:本题考查了翻折变换的知识,解答本题的关键是判断出点P是三角形的内心,注意熟练掌握三角形的内角和定理,难度一般.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
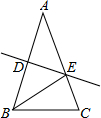 如图,等腰△ABC中,AB=AC,∠A=20°.线段AB的垂直平分线交AB于D,交AC于E,连接BE,则∠CBE等于( )
如图,等腰△ABC中,AB=AC,∠A=20°.线段AB的垂直平分线交AB于D,交AC于E,连接BE,则∠CBE等于( )| A、80° | B、70° | C、60° | D、50° |
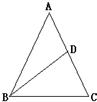 13、如图,等腰△ABC中,AB=AC,BD为腰AC的中线,将△ABC分成长12cm和9cm的两段,则等腰△ABC的腰长为
13、如图,等腰△ABC中,AB=AC,BD为腰AC的中线,将△ABC分成长12cm和9cm的两段,则等腰△ABC的腰长为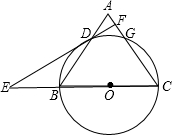 如图,等腰△ABC中,AC=BC=10,AB=12,以BC为直径作⊙0交AB于D,交AC于G,DF⊥AC,垂足为F,交CB的延长线于点E,则sinE=
如图,等腰△ABC中,AC=BC=10,AB=12,以BC为直径作⊙0交AB于D,交AC于G,DF⊥AC,垂足为F,交CB的延长线于点E,则sinE= 如图,等腰△ABC中,AB=AC,D为BC中点,E为射线AD上一点.
如图,等腰△ABC中,AB=AC,D为BC中点,E为射线AD上一点. 如图,等腰△ABC中,AB=AC,D、E分别为AC、AB的中点.
如图,等腰△ABC中,AB=AC,D、E分别为AC、AB的中点.