题目内容

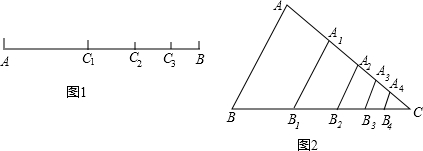
“数缺形时少直观，形少数时难入微”．小明学习上爱动脑，在计算
1
4
+
1
42
+…+
1
4n
+…的值时构造了这样一个图形：如图，正△ABC面积为
1
3
，分别取AC、BC两边的中点D、E，再分别取CD、CE的中点，依次取下去…，能直观地求出它的值．也请你根据这个图形计算：
1
4
+
1
42
+…+
1
4n
+…=
 
．
精英家教网
分析：根据相似三角形面积之比等于相似比的平方，找规律求解．
解答：解：设第n个小三角形的面积为sn，则sn=
4-n
3

根据中位线定理，得出小三角形的面积是对应梯形面积的
1
3

即sn=
1
3
•
4-n-1-4-n
3
=
4-n-1-4-n
9

那么，s1+s2+s3+…+sn=
1
9
（1-4-1+4-1-4-2+…+4-n-2-4-n-1+4-n-1-4-n）=
1-4-n
9

同时，s1+s2+s3+…+sn=
4-1+4-2+4-3+…+4-n
3

以上两式联立解得：
1
4
+
1
42
+…+
1
4n
+…=
1-4-n
3
点评：此题主要是根据相似三角形面积之比等于相似比的平方进行分析计算．
练习册系列答案
相关题目
阅读题：我国著名数学家华罗庚说过：“数缺形时少直观，形小数时难入微，数形结合百般好，隔离分家事万休．”数形结合的基本思想，就是在研究问题的过程中，注意把数和形结合起来考察，斟酌问题的具体情形，把图形性质的问题转化为数量关系的问题转化为图形性质的问题，使复杂问题简单化，抽象问题具体化，化难为易，获得简便易行的成功方案．
例：求1+2+3+4+…+n的值，其中n是正整数；
如果采用数形结合的方法，现利用图形的性质来求1+2+3+4+…+n的值，方案如下：
如图，斜线左边的三角形图案是由上到下每层依次分别为1，2，3…n个小圆圈的个数恰好为所求式子1+2+3+4+…+n的值，为求式子的值，现把左边三角形倒放于斜线右边，与原三角形组成一个平行四边形小圆圈的总个数为n（n+1）个，因此，组成一个三角形小圆圈的个数为
n(n+1)
2
，即1+2+3+4+…+n=
n(n+1)
2

①仿照上述数形结合的思想方法，设计相关图形，求1+3+5+7+…+（2n-1）的值，其中n为正整数（要求画出图形，写出结果即可）
②试设计另外一种图形，求1+3+5+7+…+（2n-1）的值，其中n是正整数（要求画出图形，写出结果即可）
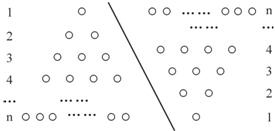
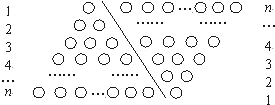精英家教网
我国著名数学家华罗庚曾说过：“数缺形时少直观，形少数时难入微；数形结合百般好，隔离分家万事休”．数学中，数和形是两个最主要的研究对象，它们之间有着十分密切的联系，在一定条件下，数和形之间可以相互转化，相互渗透．
数形结合的基本思想，就是在研究问题的过程中，注意把数和形结合起来考察，斟酌问题的具体情形，把图形性质的问题转化为数量关系的问题，或者把数量关系的问题转化为图形性质的问题，使复杂问题简单化，抽象问题具体化，化难为易，获得简便易行的成功方案．
例如：求1+2+3+4+…+n的值，其中n是正整数．
对于这个求和问题，如果采用纯代数的方法（首尾两头加），问题虽然可以解决，但在求和过程中，需对n的奇偶性进行讨论．
如果采用数形结合的方法，即用图形的性质来说明数量关系的事实，那就非常的直观．现利用图形的性质来求1+2+3+4+…+n的值，方案如下：如图，斜线左边的三角形图案是由上到下每层依次分别为1，2，3，…，n个小圆圈排列组成的．而组成整个三角形小圆圈的个数恰为所求式子1+2+3+4+…+n的值．为求式子的值，现把左边三角形倒放于斜线右边，与原三角形组成一个平行四边形．此时，组成平行四边形的小圆圈共有n行，每行有（n+1）个小圆圈，所以组成平行四边形小圆圈的总个数为n（n+1）个，因此，组成一个三角形小圆圈的个数为
n(n+1)
2
，即1+2+3+4+…+n=
n(n+1)
2
．
（1）仿照上述数形结合的思想方法，设计相关图形，求1+3+5+7+…+（2n-1）的值，其中n是正整数．（要求：画出图形，并利用图形做必要的推理说明）
（2）试设计另外一种图形，求1+3+5+7+…+（2n-1）的值，其中n是正整数．（要求：画出图形，精英家教网并利用图形做必要的推理说明）
“数缺形时少直观，形少数时难入微”，小明在探究
1
2
+
1
22
+…+
1
2n-1
+
1
2n
结果时，发现可利用图形的知识来解决问题．他是这样规定的：在图1中，若线段AB的长为1，C1为AB的中点，C2为C1B的中点，C3 为C2B的中点，…，Cn为Cn-1B的中点．
（1）则可以得出线段C1B=
 
，C1C2=
 
，ACn=
 
；
（2）从而发现了
1
2
+
1
22
+…+
1
2n-1
+
1
2n
=
 
；
（3）小明学习上爱动脑，经过认真思考和分析后，发现在计算
1
4
+
1
42
+
1
43
+…+
1
4n
时，也可以利用构造一个图形，通过面积来计算．他构造图形是：如图2，正△ABC面积为1，分别取AC、BC两边的中点A1、B1，再分别取A1C、B1C的中点A2、B2，依次取下去…，能直观地计算出结果．请你根据这个图形说明小明的结果：
1
4
+
1
42
+
1
43
+…+
1
4n
=
 
．
请你对小明的发现，试给出必要的说理．
精英家教网
一位老人非常喜欢孩子，每当有孩子到他家做客时，老人都要拿出糖果招待他们．来一个孩子，老人就给孩子一块糖；来两个孩子，老人就给每个孩子两块糖…
（1）第一天有a个男孩去了老人家，老人一共给了这些孩子a2块糖；
（2）第二天有b个女孩去了老人家，老人一共给了这些孩子b2块糖；
（3）第三天这（a+b）个孩子一起去了老人家，老人一共给了这些孩子（a+b）2块糖．
这些孩子第三天得到的糖果数与前两天他们得到的糖果总数相比哪个多，哪个少？为什么？经过思考可知，a个男孩每人多得了b块糖，b个女孩每人多得了a块糖，因此多得了ab+ab=2ab块糖，即有（a+b）2=a2+b2+2ab．
我国著名数学家华罗庚曾说过：“数缺形时少直观，形少数时难入微；数形结合百般好，隔离分家万事休”．在一定条件下，数和形之间可以相互转化，相互渗透．
体会数形结合思想的内涵，试设计一种图形来说明（a+b）2=a2+b2+2ab．（要求：画出图形，并利用图形作必要的推理说明）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网