题目内容
当x为实数时，求函数y=| x2-2x-2 | x2+2x+1 |
分析：将原函数转化为关于自变量的二次方程，应用二次方程的根的判别式△=b2-4ac≥0，从而确定原函数的值域．
解答：解：由函数y=
，得
（y-1）x2+2（y+1）x+y+2=0，①
∵x为实数，
∴方程①有实数解，
∴△=b2-4ac≥0，即4（y+1）2-4（y-1）（y+2）≥0，
∴y≥-3；
∴函数y=
的最小值是-3．
| x2-2x-2 |
| x2+2x+1 |
（y-1）x2+2（y+1）x+y+2=0，①
∵x为实数，
∴方程①有实数解，
∴△=b2-4ac≥0，即4（y+1）2-4（y-1）（y+2）≥0，
∴y≥-3；
∴函数y=
| x2-2x-2 |
| x2+2x+1 |
点评：本题考查了函数最值问题．解题时，将函数关系转化为二次方程F（x，y）=0，由于方程有实数解，故其判别式为非负数，可求得函数的值域．常适用于形如“y=
或y=ax+b±
”的函数．
| ax2+bx+c |
| dx2+ex+f |
| cx2+dx+e |
练习册系列答案
相关题目
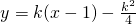与抛物线y=ax2+bx+c有且只有一个公共点，求a，b，c的值．
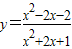的最值？