��Ŀ����
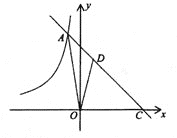
����Ŀ����ͼ��������![]() ��ֱ��
��ֱ��![]() ����A��B���㣬��x����D��C���㣬����
����A��B���㣬��x����D��C���㣬����![]() ��
��![]() ����֪
����֪![]() ��
��![]() ��
��
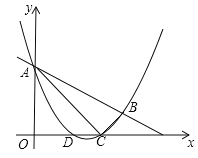
��1���������ߵĽ���ʽ��
��2��PΪy���Ҳ���������һ���㣬����![]() ������P��
������P��![]() ��y���ڵ�Q���ʣ��Ƿ���ڵ�Pʹ����A��P��QΪ������������
��y���ڵ�Q���ʣ��Ƿ���ڵ�Pʹ����A��P��QΪ������������![]() ���ƣ������ڣ���������з��������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
���ƣ������ڣ���������з��������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
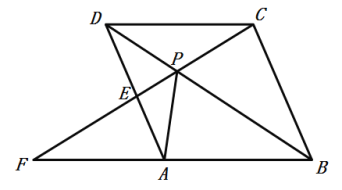
��3����EΪ�߶�![]() ��һ�㣨�����˵㣩������
��һ�㣨�����˵㣩������![]() ��һ����M�ӵ�D���������߶�
��һ����M�ӵ�D���������߶�![]() ��ÿ��һ����λ�ٶ��˶���E�㣬�����߶�
��ÿ��һ����λ�ٶ��˶���E�㣬�����߶�![]() ��ÿ��
��ÿ��![]() ����λ���ٶ��˶���A��ֹͣ������E�������Ƕ���ʱ����M�������˶�����ʱ���٣�
����λ���ٶ��˶���A��ֹͣ������E�������Ƕ���ʱ����M�������˶�����ʱ���٣�
���𰸡���1��![]() ����2�����ڣ�����P������Ϊ��11��36����
����2�����ڣ�����P������Ϊ��11��36����![]() ��
��![]() ����
����![]() ��
��![]() ������3������E������Ϊ��2��1��ʱ����M�������˶�����ʱ������
������3������E������Ϊ��2��1��ʱ����M�������˶�����ʱ������
��������
��1����A��C������������߽���ʽ�����ɵõ�����m��n�ķ����飬�ⷽ���鼴�����m��n��ֵ�������ɵý����
��2�������ֱ��AB�������ߵĽ���B�����꣬�����ù��ɶ����涨���жϳ���ABC��ֱ�������Σ��Ӷ���ACB��90�㣻����P��PG��y����G�����P�ĺ�����Ϊx���ٷֵ�G�ڵ�A���·��͵�G�ڵ�A���Ϸ����ֱ��������������ε������ú�x�Ĵ���ʽ��ʾ����P�����꣬Ȼ����������ߵĽ���ʽ�������x��ֵ�����⼴�ý����
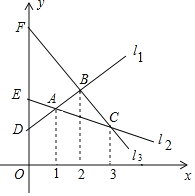
��3����ͼ3����A������AF��x�ᣬ��D������DF��y�ᣬDF��AC���ڵ�E��DF��AF���ڵ�F������õ�M�������˶��е���ʱΪ��t��![]() ��DE+EF=DF����ʱ��M�������˶��е���ʱ���٣�Ȼ�������D�����D�ĺ��������ֱ��AC����ʽ����������.
��DE+EF=DF����ʱ��M�������˶��е���ʱ���٣�Ȼ�������D�����D�ĺ��������ֱ��AC����ʽ����������.
�⣺��1����![]() ��
��![]() ���������ߵĽ���ʽ���ã�
���������ߵĽ���ʽ���ã�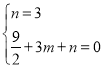 ����ã�
����ã� ��
��
�������ߵĽ���ʽΪ��![]() ��
��
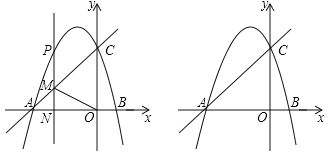
��2�����ڵ�P��ʹ����A��P��QΪ��������������ACB���ƣ�
���� ����ã�
����ã�![]() ��
��![]() �����B��������4��1����
�����B��������4��1����
��C��3��0����B��4��1����A��0��3����
��AB2��20��BC2��2��AC2��18��
��BC2+AC2��AB2�����ABC��ֱ�������Σ�
���ACB��90�㣬��tan��BAC��![]() ��
��
����P��PG��y����G�����PGA��90�㣮
���P�ĺ�����Ϊx����P��y���Ҳ�ɵ�x��0����PG��x��
��PQ��PA����ACB��90�㣬���APQ����ACB��90�㣮
����G�ڵ�A���·���
����ͼ2�٣�����PAQ����CABʱ�����PAQ�ס�CAB��
�ߡ�PGA����ACB��90�㣬��PAQ����CAB��
���PGA�ס�BCA����![]() ��
��
��AG��3PG��3x����P��x��3��3x����
��P��x��3��3x������![]() ����
����![]() ��
��
��ã�x1��0����ȥ����x2����1����ȥ����
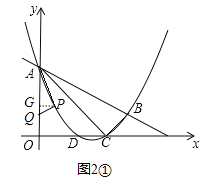
����ͼ2�ڣ�����PAQ����CBAʱ�����PAQ�ס�CBA��
ͬ���ɵã�AG��![]() PG��
PG��![]() x����P��x��3��
x����P��x��3��![]() x����
x����
��P��x��3��![]() x������
x������![]() ����
����![]() ��
��
��ã�x1��0����ȥ����x2��![]() ��
��
��P��![]() ��
��![]() ����
����

����G�ڵ�A���Ϸ���
�ٵ���PAQ����CABʱ�����PAQ�ס�CAB��
�ߡ�PGA�ס�BCA����![]() ��
��
��AG��3PG��3x����P��x��3+3x����
��P��x��3+3x������![]() ����
����![]() ��
��
��ã�x1��0����ȥ����x2��11��
���P��������11��36����
�ڵ���PAQ����CBAʱ�����PAQ�ס�CBA��
ͬ���ɵã�AG��![]() PG��
PG��![]() x����P��x��3+
x����P��x��3+![]() x����
x����
��P��x��3+![]() x������
x������![]() ����
����![]() ��
��
��ã�x1��0����ȥ����x2��![]() ��
��
��P��![]() ��
��![]() ����
����
�������������������ĵ�P������Ϊ��11��36����![]() ��
��![]() ����
����![]() ��
��![]() ����
����
��3����ͼ3����A������AF��x�ᣬ��D������DF��y�ᣬDF��AC���ڵ�E��DF��AF���ڵ�F��
��A��0��3����C��3��0������lAC��y����x+3��
��OA��OC����AOC��90�㣬���ACO��45�㣬
��AF��OC�����FAE��45�㣬
��EF��AEsin45�㣽![]() ��
��
���M�������˶��е���ʱΪ��t��![]() ��DE+EF=DF������AF��DFʱ��DE+EFȡ����СֵDF����ʱ��M�������˶��е���ʱ���٣�
��DE+EF=DF������AF��DFʱ��DE+EFȡ����СֵDF����ʱ��M�������˶��е���ʱ���٣�
�������ߵĽ���ʽΪ![]() ����y=0����
����y=0����![]() ����ã�
����ã�![]() ��
��
��D������Ϊ��2��0������E�������Ϊ2����x��2����lAC��y����x+3����y��1������E��2��1����
������E������Ϊ��2��1��ʱ����M�������˶�����ʱ���٣�