题目内容
如图,△ABC内接于⊙O,CA=CB,CD∥AB且与OA的延长线交于点D.

(1)判断CD与⊙O的位置关系,并说明理由;
(2)若∠ACB=120°,OA=2,求CD的长.

(1)判断CD与⊙O的位置关系,并说明理由;
(2)若∠ACB=120°,OA=2,求CD的长.
(1) 相切.理由见解析 (2)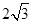
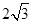
解: (1) CD与⊙O的位置关系是相切.理由如下:
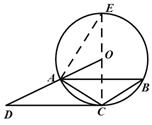
如图,作直径CE,连接AE.
∵CE是直径,∴∠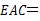 90°,∴∠
90°,∴∠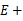 ∠
∠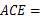 90°.
90°.
∵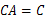 B,∴∠
B,∴∠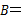 ∠
∠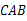 .
.
∵AB∥CD,∴∠ ∠
∠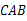 . ∵∠
. ∵∠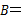 ∠
∠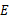 ,∴∠
,∴∠ ∠
∠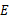 ,
,
∴ ∠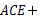 ∠
∠ 90°,即∠
90°,即∠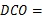 90°,
90°,
∴ OC⊥DC,∴CD与⊙O相切.
(2)∵CD∥AB,OC⊥DC,∴OC⊥AB.
又∠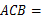 120°,∴∠
120°,∴∠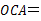 ∠
∠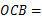 60°.
60°.
∵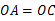 ,∴△OAC是等边三角形,∴∠
,∴△OAC是等边三角形,∴∠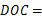 60°.
60°.
在Rt△DCO中,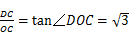 ,
,
∴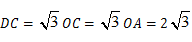 .
.
如图,作直径CE,连接AE.

∵CE是直径,∴∠
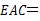 90°,∴∠
90°,∴∠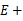 ∠
∠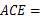 90°.
90°. ∵
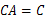 B,∴∠
B,∴∠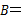 ∠
∠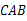 .
.∵AB∥CD,∴∠
 ∠
∠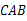 . ∵∠
. ∵∠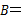 ∠
∠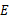 ,∴∠
,∴∠ ∠
∠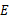 ,
,∴ ∠
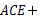 ∠
∠ 90°,即∠
90°,即∠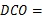 90°,
90°,∴ OC⊥DC,∴CD与⊙O相切.
(2)∵CD∥AB,OC⊥DC,∴OC⊥AB.
又∠
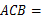 120°,∴∠
120°,∴∠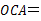 ∠
∠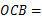 60°.
60°.∵
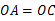 ,∴△OAC是等边三角形,∴∠
,∴△OAC是等边三角形,∴∠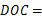 60°.
60°. 在Rt△DCO中,
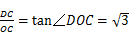 ,
,∴
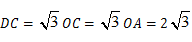 .
.
练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目


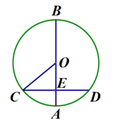
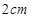 的刻度尺在圆形光盘上移动,当刻度尺的一边与光盘相切时,另一边与光盘边缘两个交点处的读数恰好是“
的刻度尺在圆形光盘上移动,当刻度尺的一边与光盘相切时,另一边与光盘边缘两个交点处的读数恰好是“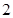 ”和“
”和“ ”(单位:
”(单位: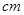 ),那么该光盘的直径为
),那么该光盘的直径为 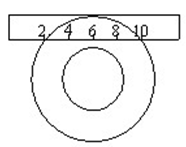
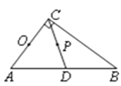
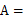 50°,∠
50°,∠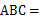 60°,
60°,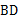 是圆
是圆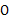 的直径,
的直径,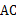 于点
于点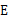 ,连结
,连结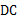 ,则∠
,则∠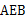 等于( )
等于( )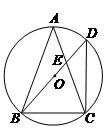
 ;图②中的四个圆的半径相等,并依次外切,且与正方形的边相切,设这四个圆的周长和为
;图②中的四个圆的半径相等,并依次外切,且与正方形的边相切,设这四个圆的周长和为 ;图③中的九个圆的半径相等,并依次外切,且与正方形的边相切,设这九个圆的周长和为
;图③中的九个圆的半径相等,并依次外切,且与正方形的边相切,设这九个圆的周长和为 ;…,依此规律,当正方形边长为2时,
;…,依此规律,当正方形边长为2时, = _______.
= _______.