Question

【题目】已知：如图1，抛物线的顶点为M，平行于x轴的直线与该抛物线交于点A，B（点A在点B左侧），根据对称性△AMB恒为等腰三角形，我们规定：当△AMB为直角三角形时，就称△AMB为该抛物线的“完美三角形”．

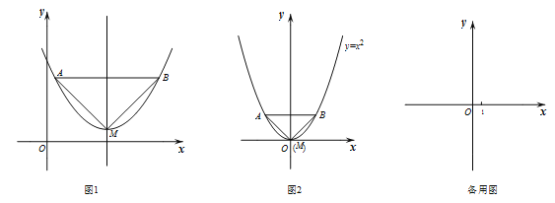
（1）①如图2，求出抛物线的“完美三角形”斜边AB的长；

②抛物线与的“完美三角形”的斜边长的数量关系是 ；

（2）若抛物线的“完美三角形”的斜边长为4，求a的值；

（3）若抛物线的“完美三角形”斜边长为n，且的最大值为-1，求m，n的值．

Answer 1

【答案】（1）、AB=2；相等；（2）、a=±；（3）、，∴．

【解析】

试题分析：（1）、过点B作BN⊥x轴于N，由题意可知△AMB为等腰直角三角形，设出点B的坐标为（n，－n），根据二次函数得出n的值，然后得出AB的值；（2）、根据抛物线的性质相同得出抛物线的完美三角形全等，从而得出点B的坐标，得出a的值；（3）、根据最大值得出mn－4m－1=0，根据抛物线的完美三角形的斜边长为n得出点B的坐标，然后代入抛物线求出m和n的值.

试题解析：（1）、①过点B作BN⊥x轴于N，由题意可知△AMB为等腰直角三角形，AB∥x轴，

易证MN=BN，设B点坐标为（n，-n），代入抛物线，得，

∴，（舍去），∴抛物线的“完美三角形”的斜边

②相等；

（2）、∵抛物线与抛物线的形状相同，

∴抛物线与抛物线的“完美三角形”全等，

∵抛物线的“完美三角形”斜边的长为4，∴抛物线的“完美三角形”斜边的长为4，

∴B点坐标为（2，2）或（2，-2），∴．

（3）、∵的最大值为-1，∴，

∴，∵抛物线的“完美三角形”斜边长为n，

∴抛物线的“完美三角形”斜边长为n，∴B点坐标为，

∴代入抛物线，得，∴（不合题意舍去），

∴，∴