题目内容
在△ABC中，∠A=40°，高BE、CF交于点O，求∠BOC的度数．
考点：三角形内角和定理
专题：
分析：分为两种情况，化成图形后根据内角和定理求出即可．
解答：解：
分为两种情况：①如图1，∵高BE、CF交于点O，
∴∠AFO=∠AEO=90°，
∵∠A=40°，
∴∠BOC=∠EOF=360°-90°-90°-40°=140°；
②如图2，∵高BE、CF交于点O，
∴∠BFO=∠AEB=90°，
∵∠A=40°，∠ABE=∠OBF，
∴∠BOC=∠A=40°；
即∠BCO=140°或40°．
分为两种情况：①如图1，∵高BE、CF交于点O，
∴∠AFO=∠AEO=90°，
∵∠A=40°，
∴∠BOC=∠EOF=360°-90°-90°-40°=140°；
②如图2，∵高BE、CF交于点O，
∴∠BFO=∠AEB=90°，
∵∠A=40°，∠ABE=∠OBF，
∴∠BOC=∠A=40°；
即∠BCO=140°或40°．
点评：本题考查了对三角形内角和定理和垂直定义的应用，注意：三角形的内角和等于180°．
练习册系列答案
相关题目
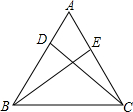如图，若AB=AC，