题目内容

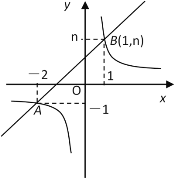
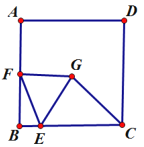
【题目】如图，正方形中边长为，为上一点，且，为边上的一个动点，连接,以为边向右侧作等边,连接,则的最小值为__________．

【答案】

【解析】

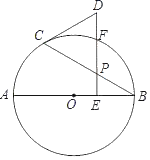
由题意分析可知，点F为主动点，G为从动点，所以以点E为旋转中心构造全等关系，得到点G的运动轨迹，之后通过垂线段最短构造直角三角形获得CG最小值．

由题意可知，点F是主动点，点G是从动点，点F在线段上运动，点G也一定在直线轨迹上运动

将△EFB绕点E旋转60°，使EF与EG重合，得到△EFB≌△EHG

从而可知△EBH为等边三角形，点G在垂直于HE的直线HN上

作CM⊥HN，则CM即为CG的最小值

作EP⊥CM，可知四边形HEPM为矩形，

则CM＝MP＋CP＝HE＋EC＝BE＋EC=1.5+＝=

故答案为．

练习册系列答案
相关题目

【题目】如图，一次函数的图象与反比例函数的图象交于A（-2，-1）、B（1，n）两点。

(1)利用图中条件求反比例函数和一次函数的解析式；

(2)根据图象写出使一次函数的值大于反比例函数的值的的取值范围．

【题目】如图，在△ABC中，点D，E分别在边AB、AC上，DC与BE相交于点O，且DO＝2，BO＝DC＝6，OE＝3．

（1）求证：DE∥BC；

（2）如果四边形BCED的面积比△ADE的面积大12，求△ABC的面积．

【题目】（1）解方程：（x+1）（x+3）＝15

（2）解方程：3x2﹣2x＝2

（3）解不等式组

【题目】已知二次函数y=ax2+2ax+3a2+3（其中x是自变量），当x≥2时，y随x的增大而增大，且-2≤x≤1时，y的最大值为9，则a的值为　　

A. 1或 B. -或 C. D. 1

【题目】已知四边形ABCD的对角线AC、BD相交于点O，下列条件中，不能判定四边形ABCD是平行四边形的是（　　）

A. ，

B. ，

C. ，

D. ，

【题目】如图，点C为线段AB上一点，分别以AB、AC、CB为底作顶角为120°的等腰三角形，顶角顶点分别为D、E、F（点E、F在AB的同侧，点D在另一侧）

（1）如图1，若点C是AB的中点，则∠CED=______°；

（2）如图2．若点C不是AB的中点

①求证：△DEF为等边三角形；

②连接CD，若∠ADC=90°，AD=，请求出DE的长．

【题目】如图，已知AB是⊙O的直径，点P是弦BC上一动点（不与端点重合），过点P作PE⊥AB于点E，延长EP交于点F，交过点C的切线于点D．

（1）求证：△DCP是等腰三角形；

（2）若OA＝6，∠CBA＝30°．

①当OE＝EB时，求DC的长；

②当的长为多少时，以点B，O，C，F为顶点的四边形是菱形？

【题目】如图（1）是一款手机支架，忽略支管的粗细，得到它的简化结构图如图（2）所示．已知支架底部支架CD平行于水平面，EF⊥OE，GF⊥EF，支架可绕点O旋转，OE＝20cm，EF＝20cm．如图（3）若将支架上部绕O点逆时针旋转，当点G落在直线CD上时，测量得∠EOG＝65°．

（1）求FG的长度（结果精确到0.1）；

（2）将支架由图（3）转到图（4）的位置，若此时F、O两点所在的直线恰好于CD垂直，点F的运动路线的长度称为点F的路径长，求点F的路径长．

（参考数据：sin65°≈0.91，cos65°≈0.42，tan65°≈2.14，1.73）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网