题目内容
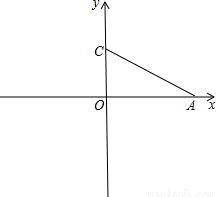
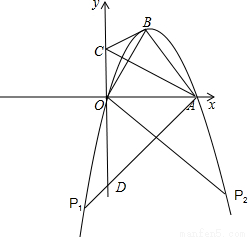
如图,在直角坐标系xoy中,点A在x轴的正半轴上,点C在y轴上,且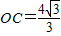 ,tan∠OAC=
,tan∠OAC=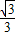 ,将△OAC沿AC翻折使点O落在坐标平面内的B点处.
,将△OAC沿AC翻折使点O落在坐标平面内的B点处.(1)求B点的坐标;
(2)二次函数y=ax2+bx+c的图象经过O、B、A三点,求这个二次函数的解析式;
(3)在(2)中的二次函数图象上是否存在一点P,使以P、A、B、O为顶点的四边形为梯形?若存在,求出P点坐标;若不存在,说明理由.
【答案】分析:(1)由tan∠OAC= ,OC=
,OC= ,即可得∠OAC=30°,OA=4,又由将△OAC沿AC翻折使点O落在坐标平面内的B点处,根据折叠的性质,易得△OAB是等边三角形,即可求得点B的坐标;
,即可得∠OAC=30°,OA=4,又由将△OAC沿AC翻折使点O落在坐标平面内的B点处,根据折叠的性质,易得△OAB是等边三角形,即可求得点B的坐标;
(2)利用待定系数法即可求得这个二次函数的解析式;
(3)由B为抛物线顶点,可得OA不可能为梯形的底,然后分别从①当OB∥P1A时与②当OP2∥BA时去分析求解即可求得答案.
解答:解:(1)∵tan∠OAC=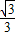 ,
,
∴∠OAC=30°
∵OC=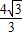 ,
,
∴OA=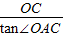 =4,
=4,
由△OAC沿AC翻折知,OB⊥AC,
∴∠BOA=60°,∠OAB=2∠OAC=60°,
∴△OAB是等边三角形,
∴OB=OA=4,
∵xB=OB•cos∠BOA=2,yB=OB•sin∠BOA=2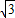 ,
,
∴B(2,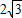 );
);
(2)∵二次函数y=ax2+bx+c的图象经过O、B、A三点,
∴设其为y=ax2+bx,
∵A(4,0),B(2,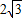 ),
),
将其代入,得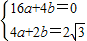 ,
,
解得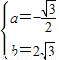 ,
,
∴y=-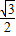 x2+2
x2+2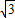 x;
x;
(3)若存在点P使四边形PABO为梯形,
∵B为抛物线顶点,
∴OA不可能为梯形的底,
①当OB∥P1A时,有∠OAD=60°,
设AP1交y轴于点D,
∵OA=4,
∴D(0,-4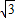 )
)
设过A、D的直线解析式为y=kx+b(k≠0),
∴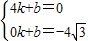 ,
,
解得: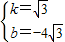 ,
,
∴直线AD的解析式为:y=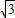 x-4
x-4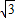 ,
,
∵P1是二次函数图象与直线AD的交点,
∴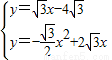 ,
,
解得: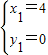 或
或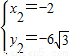 ,
,
∵A(4,0),
∴P1(-2,-6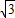 );
);
过P1作PM⊥x轴于M点,则线段P1M=6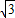 ,
,
∴线段P1A=12,OB=4,
在四边形P1ABO中,BO∥AP1,且BO≠AP1,
∴四边形P1ABO是梯形;
②当OP2∥BA时,
∵直线AB的解析式为:y=-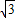 x+4
x+4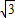 ,
,
∴直线OP2的解析式为:y=-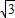 x,
x,
∴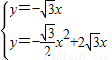 ,
,
解得: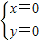 或
或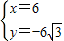 ,
,
∵O(0,0),
∴P2(6,-6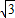 ),
),
∴OP2=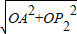 =12,
=12,
∵AB=4,
∴四边形P2ABO是梯形.
综上:P1(-2,-6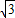 ),P2(6,-6
),P2(6,-6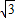 ).
).
点评:此题考查了待定系数法求函数的解析式、等边三角形的判定与性质、梯形的性质、勾股定理以及三角函数等知识.此题综合性很强,难度较大,注意掌握数形结合思想、分类讨论思想与方程思想的应用.
 ,OC=
,OC= ,即可得∠OAC=30°,OA=4,又由将△OAC沿AC翻折使点O落在坐标平面内的B点处,根据折叠的性质,易得△OAB是等边三角形,即可求得点B的坐标;
,即可得∠OAC=30°,OA=4,又由将△OAC沿AC翻折使点O落在坐标平面内的B点处,根据折叠的性质,易得△OAB是等边三角形,即可求得点B的坐标;(2)利用待定系数法即可求得这个二次函数的解析式;
(3)由B为抛物线顶点,可得OA不可能为梯形的底,然后分别从①当OB∥P1A时与②当OP2∥BA时去分析求解即可求得答案.
解答:解:(1)∵tan∠OAC=
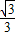 ,
,∴∠OAC=30°
∵OC=
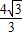 ,
,∴OA=
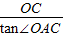 =4,
=4,由△OAC沿AC翻折知,OB⊥AC,
∴∠BOA=60°,∠OAB=2∠OAC=60°,
∴△OAB是等边三角形,
∴OB=OA=4,
∵xB=OB•cos∠BOA=2,yB=OB•sin∠BOA=2
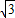 ,
,∴B(2,
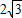 );
);(2)∵二次函数y=ax2+bx+c的图象经过O、B、A三点,
∴设其为y=ax2+bx,
∵A(4,0),B(2,
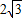 ),
),将其代入,得
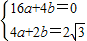 ,
,解得
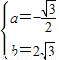 ,
,∴y=-
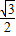 x2+2
x2+2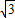 x;
x;(3)若存在点P使四边形PABO为梯形,
∵B为抛物线顶点,
∴OA不可能为梯形的底,
①当OB∥P1A时,有∠OAD=60°,
设AP1交y轴于点D,
∵OA=4,
∴D(0,-4
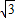 )
)
设过A、D的直线解析式为y=kx+b(k≠0),
∴
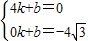 ,
,解得:
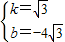 ,
,∴直线AD的解析式为:y=
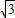 x-4
x-4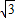 ,
,∵P1是二次函数图象与直线AD的交点,
∴
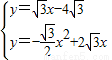 ,
,解得:
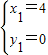 或
或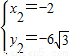 ,
,∵A(4,0),
∴P1(-2,-6
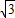 );
);过P1作PM⊥x轴于M点,则线段P1M=6
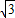 ,
,∴线段P1A=12,OB=4,
在四边形P1ABO中,BO∥AP1,且BO≠AP1,
∴四边形P1ABO是梯形;
②当OP2∥BA时,
∵直线AB的解析式为:y=-
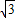 x+4
x+4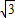 ,
,∴直线OP2的解析式为:y=-
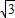 x,
x,∴
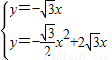 ,
,解得:
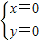 或
或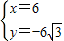 ,
,∵O(0,0),
∴P2(6,-6
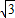 ),
),∴OP2=
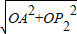 =12,
=12,∵AB=4,
∴四边形P2ABO是梯形.
综上:P1(-2,-6
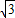 ),P2(6,-6
),P2(6,-6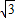 ).
).点评:此题考查了待定系数法求函数的解析式、等边三角形的判定与性质、梯形的性质、勾股定理以及三角函数等知识.此题综合性很强,难度较大,注意掌握数形结合思想、分类讨论思想与方程思想的应用.

练习册系列答案
相关题目
 是方程x2-10x+16=0的两个根,且x1<x2,连接MC,过A、B、C三点的抛物线的顶点为N.
是方程x2-10x+16=0的两个根,且x1<x2,连接MC,过A、B、C三点的抛物线的顶点为N.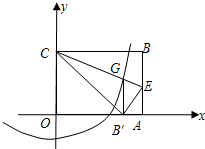 半径的圆与抛物线是否还有除G点以外的交点?若有,请找出这个交点坐标.
半径的圆与抛物线是否还有除G点以外的交点?若有,请找出这个交点坐标. 已如:如图,在直角坐标系中,以y轴上的点C为圆心,2为半径的圆与x轴相切于原点O,AB为⊙C的直径,PA切⊙O于点A,交x轴的负半轴于点P,连接PC交OA于点D.
已如:如图,在直角坐标系中,以y轴上的点C为圆心,2为半径的圆与x轴相切于原点O,AB为⊙C的直径,PA切⊙O于点A,交x轴的负半轴于点P,连接PC交OA于点D. 如图:在直角坐标系中描出A(-4,-4),B(1,-4),C(2,-1),D(-3,-1)四个点.
如图:在直角坐标系中描出A(-4,-4),B(1,-4),C(2,-1),D(-3,-1)四个点.