题目内容
 如图,学校有四栋学生宿舍,分别用A、B、C、D表示,建立如图所示的直角坐标系,四地的坐标分别为A(-3,2)、B(1,1)、C(-5,-3)、D(-1,-4).为了方便学生,学校要新建一个食堂,你认为新建食堂修在哪里,对大家都方便?在图上指出食堂的具体位置和坐标.
如图,学校有四栋学生宿舍,分别用A、B、C、D表示,建立如图所示的直角坐标系,四地的坐标分别为A(-3,2)、B(1,1)、C(-5,-3)、D(-1,-4).为了方便学生,学校要新建一个食堂,你认为新建食堂修在哪里,对大家都方便?在图上指出食堂的具体位置和坐标.
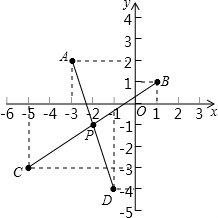 解:连接AD,BC,相交于点P,
解:连接AD,BC,相交于点P,则点P处就是所要求的食堂的位置.
设直线AD的解析式为y=kx+b,
∵A(-3,2),D(-1,-4),
∴
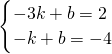 ,
,解得
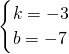 ,
,∴直线AD的解析式是y=-3x-7①,
同理设直线BC的解析式是y=ax+c,
∵B(1,1)、C(-5,-3),
∴
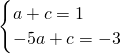 ,
,解得
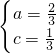 ,
,∴直线BC的解析式是y=
 x+
x+ ②,
②,①②联立方程组得,
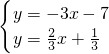 ,
,解得
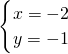 ,
,∴交点P的坐标为(-2,-1).
分析:连接AD、BC相交于点P,根据两点之间线段最短,在点P处A、D两栋宿舍的学生所走路程之和最短,B、C两栋宿舍的学生所走路程之和也最短,所以对大家都方便.
点评:本题考查了应用与设计作图,主要利用了两点之间线段最短的性质,还考查了待定系数法求函数解析式以及相交直线的交点的求法,属于小综合题,但难度不大,要细心计算.

练习册系列答案
相关题目
 如图,学校有四栋学生宿舍,分别用A、B、C、D表示,建立如图所示的直角坐标系,四地的坐标分别为A(-3,2)、B(1,1)、C(-5,-3)、D(-1,-4).为了方便学生,学校要新建一个食堂,你认为新建食堂修在哪里,对大家都方便?在图上指出食堂的具体位置和坐标.
如图,学校有四栋学生宿舍,分别用A、B、C、D表示,建立如图所示的直角坐标系,四地的坐标分别为A(-3,2)、B(1,1)、C(-5,-3)、D(-1,-4).为了方便学生,学校要新建一个食堂,你认为新建食堂修在哪里,对大家都方便?在图上指出食堂的具体位置和坐标.