题目内容
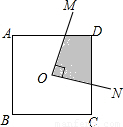
 如图,若O是正方形ABCD的中心,直角∠MON绕O点旋转,则∠MON与正方形围成的四边形的面积是正方形ABCD面积的
如图,若O是正方形ABCD的中心,直角∠MON绕O点旋转,则∠MON与正方形围成的四边形的面积是正方形ABCD面积的| 1 |
| 4 |
| 1 |
| 4 |
分析:根据∠DOC=∠MON=90°,推出∠EOD=∠FOC,又有∠OCF=∠ODE,OD=OC,可证△ODE≌△OCF,根据全等三角形的面积相等,将S四边形OEDF转化为S△DOC,得出与正方形面积S的关系.
解答: 解:连接OD、OC.
解:连接OD、OC.
∵O为正方形的中心,
∴∠DOC=
=90°,
∵∠MON=90°,
∴∠FOC+∠DOF=∠EOD+∠DOF=90°,
∴∠EOD=∠FOC,
∵O为正方形ABCD的中心,
∴∠OCF=∠ODE=45°,
在△ODE和△OCF中
∵
∴△ODE≌△OCF(ASA),
∴S△EDO+S△DOF=S△FOC+S△DOF,
即 S四边形OEDF=S△DOC,
∵S△DOC=
S,
∴S四边形OEDF=
S;
故答案为:
.
 解:连接OD、OC.
解:连接OD、OC.∵O为正方形的中心,
∴∠DOC=
| 360° |
| 4 |
∵∠MON=90°,
∴∠FOC+∠DOF=∠EOD+∠DOF=90°,
∴∠EOD=∠FOC,
∵O为正方形ABCD的中心,
∴∠OCF=∠ODE=45°,
在△ODE和△OCF中
∵
|
∴△ODE≌△OCF(ASA),
∴S△EDO+S△DOF=S△FOC+S△DOF,
即 S四边形OEDF=S△DOC,
∵S△DOC=
| 1 |
| 4 |
∴S四边形OEDF=
| 1 |
| 4 |
故答案为:
| 1 |
| 4 |
点评:本题考查了旋转的性质,正方边形的性质以及全等三角形的判定与性质.关键是用旋转的观点,将四边形的面积转化为三角形的面积,得出三角形在正多边形中,所占面积的比.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
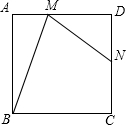 如图,四边形ABCD是正方形,点N是CD的中点,M是AD边上不同于点A、D的点,若sin∠ABM=
如图,四边形ABCD是正方形,点N是CD的中点,M是AD边上不同于点A、D的点,若sin∠ABM=
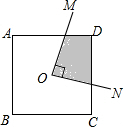 如图,若O是正方形ABCD的中心,直角∠MON绕O点旋转,则∠MON与正方形围成的四边形的面积是正方形ABCD面积的________.
如图,若O是正方形ABCD的中心,直角∠MON绕O点旋转,则∠MON与正方形围成的四边形的面积是正方形ABCD面积的________.