Question

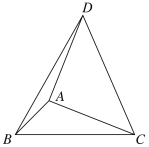
【题目】如图，在△ABC中，∠ABC=45° ， BC=4，以AC为直角边，点A为直角顶点向△ABC的外侧作等腰直角三角形ACD，连接BD，则△DBC的面积为( ) .

A.8B.10C.4D.8

Answer 1

【答案】A

【解析】

将△ABD绕着点A顺时针旋转90°得到△AEC，BD与EC交于点O，连接BE，根据旋转的性质得到AE=AB，∠BAE=∠DOC=90°，过D点作DF⊥BC，证△EBC≌BFD，可得DF=BC=4，再用三角形面积公式即可得出答案.

解：如下图所示，将△ABD绕着点A顺时针旋转90°得到△AEC，BD与EC交于点O，连接BE，

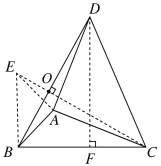
根据旋转的性质可知EC=BD，AE=AB，∠BAE=∠DOC=90°，

∴△ABE是等腰直角三角形，

∴∠ABE=45°，

又∵∠ABC=45°，

∴∠EBC=90°，

∵∠BDF+∠DBF=90°，∠ECB+∠DBF=90°，

∴∠BDF=∠ECB

在△EBC和△BFD中

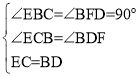
∴△EBC≌△BFD（AAS）

∴DF=BC=4

∴△DBC的面积=

故选A.