Question

【题目】如图，平面直角坐标系中，若点A（3，0）、B（4，1）到一次函数y＝kx+4（k≠0）图象的距离相等，则k的值为_____．

Answer 1

【答案】k＝±1．

【解析】

根据一次函数y=kx+4(k≠0)图象一定过点(0，4)，点A(3，0)、B(4，1)到一次函数y=kx+4(k≠0)图象的距离相等，可分为两种情况进行解答，即，①当直线y=kx+4(k≠0)与直线AB平行时，②当直线y=kx+4(k≠0)与直线AB不平行时分别进行解答即可．

一次函数y=kx+4(k≠0)图象一定过(0，4)点，

①当直线y=kx+4(k≠0)与直线AB平行时，如图1，

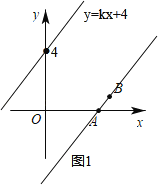
设直线AB的关系式为y=kx+b，

把A(3，0)，B(4，1)代入得，

，解得，k=1，b=﹣3，

∴一次函数y=kx+4(k≠0)中的k=1；

②当直线y=kx+4(k≠0)与直线AB不平行时，如图2，

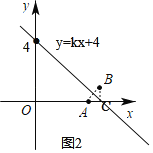
根据题意，直线y=kx+4(k≠0)垂直平分线段，此时一定经过点C，

∴点C的坐标为(4，0)，代入得，

4k+4=0，解得，k=﹣1，

因此，k=1或k=﹣1．

故答案为：k=±1．