题目内容
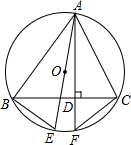如图，已知△ABC的顶点在⊙O上，AE是⊙O的直径，AD⊥BC于点D．求证：∠BAE=∠CAD．
证明：∵AE是⊙O的直径，
∴∠ABE=90°，
∴∠BAE+∠BEA=90°，
∵AD⊥BC，
∴∠ADC=90°，
∴∠CAD+∠ACB=90°，
∵∠E=∠ACB，
∴∠BAE=∠CAD．
分析：根据AE是⊙O的直径，得出∠BAE+∠BEA=90°，再根据AD⊥BC，得出∠CAD+∠ACB=90°，最后根据同弧所对的圆周角相等得出∠E=∠ACB，即可得出答案．
点评：此题考查了圆周角定理，根据圆周角定理可得到相等的角，根据等量代换可求得∠BEA=∠ACB是解题的关键．
∴∠ABE=90°，
∴∠BAE+∠BEA=90°，
∵AD⊥BC，
∴∠ADC=90°，
∴∠CAD+∠ACB=90°，
∵∠E=∠ACB，
∴∠BAE=∠CAD．
分析：根据AE是⊙O的直径，得出∠BAE+∠BEA=90°，再根据AD⊥BC，得出∠CAD+∠ACB=90°，最后根据同弧所对的圆周角相等得出∠E=∠ACB，即可得出答案．
点评：此题考查了圆周角定理，根据圆周角定理可得到相等的角，根据等量代换可求得∠BEA=∠ACB是解题的关键．
练习册系列答案
提分百分百检测卷系列答案
宝贝计划期末冲刺夺100分系列答案
能考试全能100分系列答案
相关题目
如图，已知△ABC的面积为4，且AB=AC，现将△ABC沿CA方向平移CA的长度，得到△EFA．
（2010•孝感模拟）如图，已知△ABC的三个顶点的坐标分别为A（-2，2）、B（-5，0）、C（-1，0）．
如图，已知△ABC的三个顶点的坐标分别是A（-7，1），B（-3，3），C（-2，6）．