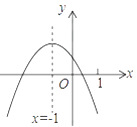题目内容
【题目】如图,在平面直角坐标系中,已知![]() ,
,![]() ,其中
,其中![]() 满足
满足![]() .
.

(1)填空:![]() _______,
_______,![]() ________;
________;
(2)若在第三象限内有一点![]() ,用含
,用含![]() 的式子表示
的式子表示![]() 的面积;
的面积;
(3)在(2)条件下,当![]() 时,点
时,点![]() 是坐标轴上的动点,当满足
是坐标轴上的动点,当满足![]() 的面积是
的面积是![]() 的面积的2倍时,求点
的面积的2倍时,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ,
,![]() ;(2)
;(2) ![]() ;(3) (
;(3) (![]() ,0)或(
,0)或(![]() ,0)或(
,0)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)
【解析】
(1)利用非负数的性质求得![]() 、
、![]() 的值,即可得出答案;
的值,即可得出答案;
(2)过M作ME⊥![]() 轴于E,根据三角形的面积公式即可得到结果;
轴于E,根据三角形的面积公式即可得到结果;
(3)分类讨论,P点可以在x轴上,也可以在y轴上,根据点的坐标特征以及面积公式求解即可.
(1)∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ;
;
(2)如图1所示,过M作CE⊥![]() 轴于E,
轴于E,

∵![]() ,
,![]() ,
,
∴A(-1,0),B(3,0),
∴OA=1,OB=3,
∴AB=4,
∵在第三象限内有一点M(-2,m),
∴ME![]() ,
,
∴S△ABM=![]() AB×ME=
AB×ME=![]() ×4×(
×4×(![]() )=
)=![]() ;
;
(2)当![]() 时,点M的坐标为(
时,点M的坐标为(![]() ,
,![]() ), S△ABM=
), S△ABM=![]() ,
,
∴![]() ,
,
设直线BM交![]() 轴于C点,
轴于C点,
①当点P在![]() 轴上时,如图:
轴上时,如图:

∵![]()
解得:PC=![]() ,
,
设直线BM的解析式为![]() ,
,
把点M(![]() ,
,![]() ), B(3,0)代入得:
), B(3,0)代入得: ,
,
解得: ,
,
∴直线BM的解析式为![]() ,
,
当![]() 时,
时,![]() ,
,
∴点C的坐标为(![]() ,
,![]() ),
),
∴OC=![]() ,
,
当点P在点C的下方时,点P的坐标为(![]() ,
,![]() ),即P(
),即P(![]() ,
,![]() ),
),
当点P在点C的上方时,点P的坐标为(![]() ,
,![]() ),即
),即![]() (
(![]() ,
,![]() ),
),
②当P在![]() 轴上且在点A的左侧时,设P点的坐标为(
轴上且在点A的左侧时,设P点的坐标为(![]() ,0),如图:
,0),如图:

∵![]() ,
,
∴PB=2AB,
∵B(3,0),AB=4,
∴![]() ,
,
∴![]() ,
,
∴P点的坐标为(![]() ,0),
,0),
当P在![]() 轴上且在点B的D右侧时,设P点的坐标为(
轴上且在点B的D右侧时,设P点的坐标为(![]() ,0),如图:
,0),如图:

同理,PB=2AB,
∵B(3,0),AB=4,
∴![]() ,
,
∴![]() ,
,
∴P点的坐标为(![]() ,0),
,0),
综合上述:P点的坐标为(![]() ,0)或(
,0)或(![]() ,0)或(
,0)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目