题目内容
已知三角形的三边之比为1：1：
，则该三角形中最大角为 度．
| 3 |
分析：根据题意等腰三角形ABC，过顶点A作AD⊥BC于点D．然后根据等腰三角形的性质以及直角三角形中特殊角的三角函数值可以求得∠BCAC的度数．
解答：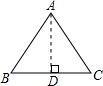
解：如图，三角形的三边之比为：AB：AC：BC=1：1：
．
∵在三角形中，大边对大角，
∴在等腰△ABC的内角中，∠BAC最大．
过A作AD⊥BC于点D．
∴BD=CD，∠BAD=∠CAD，
∴sin∠BAD=
=
=
，
∴∠BAD=60°；
同理求得∠CAD=60°，
∴∠BAC=120°；
故答案是：120°．
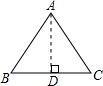解：如图，三角形的三边之比为：AB：AC：BC=1：1：| 3 |
∵在三角形中，大边对大角，
∴在等腰△ABC的内角中，∠BAC最大．
过A作AD⊥BC于点D．
∴BD=CD，∠BAD=∠CAD，
∴sin∠BAD=
| BD |
| AB |
| ||||
| 1 |
| ||
| 2 |
∴∠BAD=60°；
同理求得∠CAD=60°，
∴∠BAC=120°；
故答案是：120°．
点评：此题考查了解直角三角形．通过作辅助线AD构建直角三角形，在直角三角形中根据特殊角的三角函数的定义可以求得所求的角的度数．
练习册系列答案
阅读快车系列答案
相关题目
已知三角形的三边长之比为1：1：
，则此三角形一定是（ ）
| 2 |
| A、锐角三角形 |
| B、钝角三角形 |
| C、等边三角形 |
| D、等腰直角三角形 |
和
，那么第三边的长一定是
；