题目内容
如图，等腰△ABC中，AB=AC，∠BAC=120°，AD=DC=2，
（1）求AC的长；
（2）求△ABC的面积．
解：（1）过点A作AE⊥BC，如下图所示，
∵AB=AC，∠BAC=120°，
∴∠CAE=60°，∠C=30°，
∵AD=DC=2，
∴∠ADE=2∠C=60°，
∴∠DAE=30°，
∴ED=
AD=1，AE=
，
∴AC=2AE=2；
（2）S△ABC=BC×AE=×2CE×AE=（ED+DC）×AE=3．
分析：（1）过点A作AE⊥BC，由题给条件可求出∠DAE=30°，继而利用含30°角的直角三角形的性质求出ED和AE的值，继而求出AC的长；
（2）利用三角形的面积公式直接计算即可．
点评：本题考查勾股定理的知识，解题关键是准确作出辅助线来构造直角三角形，同时要熟练掌握含30°角的直角三角形的性质，难度一般．
∵AB=AC，∠BAC=120°，
∴∠CAE=60°，∠C=30°，
∵AD=DC=2，
∴∠ADE=2∠C=60°，
∴∠DAE=30°，
∴ED=
AD=1，AE=，∴AC=2AE=2
；（2）S△ABC=
BC×AE=×2CE×AE=（ED+DC）×AE=3．分析：（1）过点A作AE⊥BC，由题给条件可求出∠DAE=30°，继而利用含30°角的直角三角形的性质求出ED和AE的值，继而求出AC的长；
（2）利用三角形的面积公式直接计算即可．
点评：本题考查勾股定理的知识，解题关键是准确作出辅助线来构造直角三角形，同时要熟练掌握含30°角的直角三角形的性质，难度一般．
练习册系列答案
阅读快车系列答案
相关题目
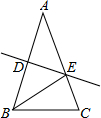如图，等腰△ABC中，AB=AC，∠A=20°．线段AB的垂直平分线交AB于D，交AC于E，连接BE，则∠CBE等于（ ）| A、80° | B、70° | C、60° | D、50° |
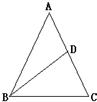13、如图，等腰△ABC中，AB=AC，BD为腰AC的中线，将△ABC分成长12cm和9cm的两段，则等腰△ABC的腰长为
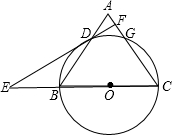如图，等腰△ABC中，AC=BC=10，AB=12，以BC为直径作⊙0交AB于D，交AC于G，DF⊥AC，垂足为F，交CB的延长线于点E，则sinE=
如图，等腰△ABC中，AB=AC，D为BC中点，E为射线AD上一点．
如图，等腰△ABC中，AB=AC，D、E分别为AC、AB的中点．