题目内容
6.有一个边长为12cm的正六边形,若要剪一张圆形纸片完全盖住这个正六边形,则这个圆形纸片的半径最小是12cm.分析 根据题意画出图形,再根据正多边形圆心角的求法求出∠AOB的度数,最后根据等腰三角形及直角三角形的性质解答即可.
解答 解:如图所示,正六边形的边长为12cm,OG⊥BC,
∵六边形ABCDEF是正六边形,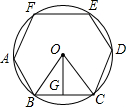
∴∠BOC=$\frac{360°}{6}$=60°,
∵OB=OC,OG⊥BC,
∴∠BOG=∠COG=$\frac{1}{2}×60°$=30°,
∵OG⊥BC,OB=OC,BC=12cm,
∴BG=$\frac{1}{2}$BC=$\frac{1}{2}$×12=6cm,
∴OB=$\frac{BG}{sin∠BOG}$=$\frac{6}{\frac{1}{2}}$=12cm,
故答案为:12cm.
点评 本题考查的是正多边形和圆,根据题意画出图形,利用直角三角形的性质及正六边形的性质解答是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.下表是北京与国外几个城市的时差,其中带正号的数表示同一时刻比北京时间早的时数,试求出:东京与巴黎的时差:8
| 城市 | 巴黎 | 纽约 | 东京 | 芝加哥 |
| 时差/时 | -7 | -13 | +1 | -14 |
14.代数式$\frac{4x}{5}$,$\frac{4}{x+2y}$,$\frac{{x}^{2}+2}{π+1}$,$\frac{5}{2}$,$\frac{1}{b}$,2x+$\frac{1}{x}$中,是分式的有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
17.轮船在顺水航行90千米比逆水航行90千米少花了3小时,已知水流速度是2千米/时,求轮船在静水中的速度.设轮船在静水中的速度为x千米/时,依据题意列方程得( )
| A. | $\frac{90}{x+2}$+3=$\frac{90}{x-2}$ | B. | $\frac{90}{x-2}$+3=$\frac{90}{x+2}$ | C. | $\frac{90}{x+3}$+2=$\frac{90}{x-3}$ | D. | $\frac{90}{x+3}$-2=$\frac{90}{x-3}$ |
 一次函数y=kx-1的图象与坐标轴分别交于A、B两点,与反比例函数y=$\frac{m}{x}$的图象在第二象限交于点C,作CD⊥x轴于点D,若OB=BD=2.
一次函数y=kx-1的图象与坐标轴分别交于A、B两点,与反比例函数y=$\frac{m}{x}$的图象在第二象限交于点C,作CD⊥x轴于点D,若OB=BD=2.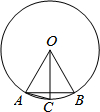 如图,在⊙O中,OA=AB,OC⊥AB,则下列结论正确的有A,B,D,F (填字母)
如图,在⊙O中,OA=AB,OC⊥AB,则下列结论正确的有A,B,D,F (填字母)  如图,在Rt△ABC中,∠C=90°,D是AC上一点,DE⊥AB于E,且DE=DC.若∠A=20°,则∠DBC的度数为35°.
如图,在Rt△ABC中,∠C=90°,D是AC上一点,DE⊥AB于E,且DE=DC.若∠A=20°,则∠DBC的度数为35°.