题目内容
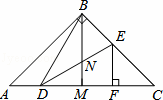
如图,抛物线y=x2+bx+c经过点A(﹣1,0),B(3,0).请解答下列问题:
(1)求抛物线的解析式;
(2)点E(2,m)在抛物线上,抛物线的对称轴与x轴交于点H,点F是AE中点,连接FH,求线段FH的长.
注:抛物线y=ax2+bx+c(a≠0)的对称轴是x=﹣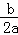 .
.

解:(1)∵抛物线y=x2+bx+c经过点A(﹣1,0),B(3,0),
∴
解得: ,
,
∴抛物线的解析式为:y=x2﹣2x﹣3;
(2)∵点E(2,m)在抛物线上,
∴m=4﹣4﹣3=﹣3,
∴E(2,﹣3),
∴BE= =
= ,
,
∵点F是AE中点,抛物线的对称轴与x轴交于点H,即H为AB的中点,
∴FH是三角形ABE的中位线,
∴FH= BE=
BE= ×
× =
= .
.

练习册系列答案
相关题目
 中,AB∥CD,
中,AB∥CD, ,
, .取
.取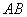 的中点
的中点 ,连接
,连接 ,再分别取
,再分别取 的中点
的中点 ,
, ,连接
,连接 ,得到四边形
,得到四边形 ,如图2;同样方法操作得到四边形
,如图2;同样方法操作得到四边形 ,如图3;…,如此进行下去,则四边形
,如图3;…,如此进行下去,则四边形 的面积为 .
的面积为 . 

 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )
 .
.