题目内容
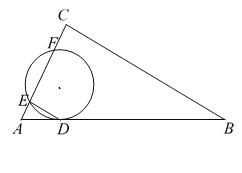
【题目】如图,圆![]() 与
与![]() 的斜边
的斜边![]() 相切于点
相切于点![]() ,与直角边
,与直角边![]() 相交于
相交于![]() 两点,连结
两点,连结![]() ,已知
,已知![]() ,圆
,圆![]() 的半径为6,弧
的半径为6,弧![]() 的长度为
的长度为![]() 。
。
(1)求证:![]() ∥
∥![]() ;
;
(2)若![]() ,求线段
,求线段![]() 的长度。
的长度。
【答案】(1)证明见解析(2)CA=10![]() ,CB=30
,CB=30
【解析】试题分析:(1)要证明DE∥BC,可证明∠EDA=∠B,由弧DE的长度为4π,可以求得∠DOE的度数,再根据切线的性质可求得∠EDA的度数,即可证明结论.
(2)根据90°的圆周角对的弦是直径,可以求得EF,的长度,借用勾股定理求得AE与CF的长度,即可得到答案.
试题解析:(1)证明:连接OE,OF,OD
∵圆![]() 的半径为6,弧
的半径为6,弧![]() 的长度为
的长度为![]()
∴![]() 即∠EOD=n=60°,OD=OE=6
即∠EOD=n=60°,OD=OE=6
∴△EOD为等边三角形
∴∠OED=∠EDO =∠EOD =60°
∵圆![]() 与
与![]() 的斜边
的斜边![]() 相切于点
相切于点![]()
∴OD⊥AB即∠ODA =90°
∴∠EDA =∠ODA -∠ODE =30°=∠B
∴![]() ∥
∥![]()

(2)解:∵![]() ∥
∥![]() ,∠C =90°∴
,∠C =90°∴
∴∠AED =∠C=90°,∠FED =180°-∠C=90°
∴FD为圆![]() 的直径,即FD过点O
的直径,即FD过点O
∴在Rt△EDF中,∠EFD =90°-∠EDF=30°
∴FD=12,EF=6![]()
∴在Rt△AED中,EA=2![]()
∴CE=AF=8![]()
∴CA=AF+AE=10![]() ,CB=
,CB=![]() AC=30
AC=30

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目