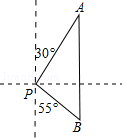题目内容
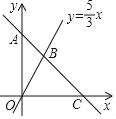
【题目】一次函数y=kx+b的图象经过点A（0，9），并且与直线y=
x相交于点B，与x轴相交于点C．
（1）若点B的横坐标为3，求B点的坐标和k，b的值；
（2）在y轴上是否存在这样的点P，使得以点P，B，A为顶点的三角形是等腰三角形？若存在，请直接写出点P坐标；若不存在，请说明理由．
（3）在直线y=kx+b上是否存在点Q，使△OBQ的面积等于
？若存在，请求出点Q的坐标；若不存在，请说明理由．
【答案】（1）B（3，5），
，b=9；（2）P1（0，9+
），P2（0，9﹣）， P3（0，
），
P4（0，
）；（3）Q（
，
）或（
，
）．
【解析】
（1）先根据函数y=
x求出B点坐标，再利用待定系数法求出k，b的值；
（2）先将两个函数组成方程组求得B点坐标，然后求出线段AB的长，再分别以A，B，P为顶点分类讨论得到P点的坐标；
（3）设Q点横坐标为a，根据点Q，C在直线
上，得到Q，C的坐标，然后分情况讨论Q点的位置，再利用三角形面积公式求解得到a的值，从而得到Q点的坐标.
解：（1）当x=3时，y=x=×3=5，即B（3，5），
把A（0，9），B（3，5）代入y=kx+b得到
，
解得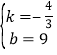
．
（2）由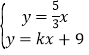
,解得
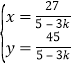，即B（
，
），
∴AB=
．
①以A为顶点时，AB=AP,（1）P点在A点上方，P1（0，9+），
（2）P点在A点下方，P2（0，9﹣）；
②以B为顶点时，BA=BP，P3（0，）；
③以P为顶点时，PA=PB，P4（0，）．
（3）设Q点的横坐标为a，
∵Q，C在直线上，
∴Q（a，ka+9），C（﹣
，0），
①当Q点在B点右侧时，
S△DBQ=
×（﹣）×（﹣ka﹣9）=
，
∴a=，
代入函数解得：Q（，）；
②当Q在点B左侧时，
S△BDQ=×（﹣）×（ka+9﹣）=，
∴a=，
代入函数解得：Q（，），
综上所述，Q（，）或
，
．
