题目内容
(本题满分12分)
设抛物线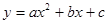 与X轴交于两不同的点
与X轴交于两不同的点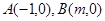 (点A在点B的左边),与y轴的交点为点C(0,-2),且∠ACB=900.
(点A在点B的左边),与y轴的交点为点C(0,-2),且∠ACB=900.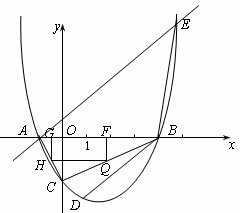
【小题1】(1)求m的值和该抛物线的解析式;
【小题2】(2)若点D为该抛物线上的一点,且横坐标为1,点E为过A点的直线y=x+1与该抛物线的另一交点.在X轴上是否存在点P,使得以P、B、D为顶点的三角形与△AEB相似,若存在,求出点P的坐标,若不存在,请说明理由.
【小题3】(3)连结AC、BC,矩形FGHQ的一边FG在线段AB上,顶点H、Q分别在线段AC、BC上,若设F点坐标为(t,0),矩形FGHQ的面积为S,当S取最大值时,连接FH并延长至点M,使HM=k·FH,若点M不在该抛物线上,求k的取值范围.
【小题1】①∵∠ACB=900,
∴OC⊥AB,可得OC2=OA·OB,OB=4,B(4,0),
设抛物线为:y=a(x+1)(x-4),点C在抛物线上,
可得a= ,∴y=
,∴y=
【小题2】②由题意可得D(1,-3),设AE与Y轴交于点N,
可得A(-1,0),N(0,1),∴OA=ON,∠EAB =450,
过D作DR⊥X轴于R,∴DR=BR=3,∠DBO =450,
∴∠DBO=∠EAB,由y=x+1和y= 可求得
可求得
E(6,7),且AE=7 ,AB=5,BD=3
,AB=5,BD=3 ,
,
设P点为(xp,0),要使△BDP∽△ABE,需要满足(1) 或(2)
或(2) .
.
若满足(1),则有 ,xp =
,xp = .若满足(2),则有
.若满足(2),则有 ,xp =
,xp = .
.
∴存在点P,使得以P、B、D为顶点的三角形与△AEB相似,P点为( ,0),(
,0),( ,0)
,0)
【小题3】③由题意可求得:AC:y= -2x-2,BC:y= x-2,可得Q(t,
x-2,可得Q(t, t-2),把y=
t-2),把y= t -2代入y= -2x-2中,
t -2代入y= -2x-2中,
得x= ,而0<t<4,FG=
,而0<t<4,FG= ,S=
,S= ·(
·( )=
)= 当t=2时,S最大.
当t=2时,S最大.
此时F(2,0),H(- ),FH=
),FH= ,直线FH为y=
,直线FH为y= .由
.由 =
= ,得x=
,得x= (舍去了正值),设FH与抛物线交于点I,过I作IJ⊥X轴于J,所以
(舍去了正值),设FH与抛物线交于点I,过I作IJ⊥X轴于J,所以 ,由于M点不在抛物线上,则k>0,且k≠
,由于M点不在抛物线上,则k>0,且k≠ .
.
解析



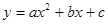 与X轴交于两不同的点
与X轴交于两不同的点 (点A在点B的左边),与y轴的交点为点C(0,-2),且∠ACB=900.
(点A在点B的左边),与y轴的交点为点C(0,-2),且∠ACB=900.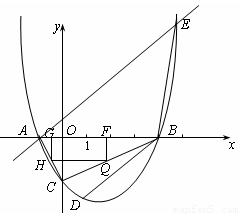
 cm,BC = 6 cm,EF = 12cm.
cm,BC = 6 cm,EF = 12cm.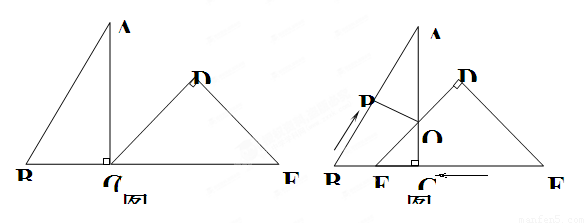
 .解答下列问题:
.解答下列问题: