题目内容
已知二次函数y=ax2+bx+c的图象过点A(-1,0)和C(0,1)(1)若此抛物线对称轴是直线x=
 ,则抛物线上关于点C的对称点的坐标是 .
,则抛物线上关于点C的对称点的坐标是 .(2)若抛物线的顶点在第一象限,设t=a+b+c,则t的取值范围为是 .
【答案】分析:(1)利用关于对称轴对称的点的坐标到对称轴的距离相等和其中一点的坐标可以求出它的对称点的坐标;
(2)根据图象经过的两点和t的值可以确定二次函数y=ax2+bx+c的图象当x=1时候的y的值的范围即可.
解答:解:(1)∵二次函数y=ax2+bx+c的图象过点C(0,1)且对称轴是直线x= ,
,
∴点C和其对称点到直线x= 的距离相等,
的距离相等,
∴抛物线上关于点C的对称点的坐标是(1,1);
(2)∵抛物线的顶点在第一象限,且二次函数y=ax2+bx+c的图象过点A(-1,0)和C(0,1),
∴当x=1时候,0<函数值<2,
∵t=a+b+c,
∴0<t<2.
故答案为:(1,1);0<t<2;
点评:主要考查了函数的单调性.二次函数y=ax2+bx+c(a,b,c为常数,a≠0),当a>0时,在对称轴左侧y随x的增大而减小,在对称轴右侧y随x的增大而增大;当a<0时,在对称轴左侧y随x的增大而增大,在对称轴右侧y随x的增大而减小.正比例函数中当k>0时,y随x的增大而增大,k<0时,y随x的增大而减小.
(2)根据图象经过的两点和t的值可以确定二次函数y=ax2+bx+c的图象当x=1时候的y的值的范围即可.
解答:解:(1)∵二次函数y=ax2+bx+c的图象过点C(0,1)且对称轴是直线x=
 ,
,∴点C和其对称点到直线x=
 的距离相等,
的距离相等,∴抛物线上关于点C的对称点的坐标是(1,1);
(2)∵抛物线的顶点在第一象限,且二次函数y=ax2+bx+c的图象过点A(-1,0)和C(0,1),
∴当x=1时候,0<函数值<2,
∵t=a+b+c,
∴0<t<2.
故答案为:(1,1);0<t<2;
点评:主要考查了函数的单调性.二次函数y=ax2+bx+c(a,b,c为常数,a≠0),当a>0时,在对称轴左侧y随x的增大而减小,在对称轴右侧y随x的增大而增大;当a<0时,在对称轴左侧y随x的增大而增大,在对称轴右侧y随x的增大而减小.正比例函数中当k>0时,y随x的增大而增大,k<0时,y随x的增大而减小.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
已知二次函数y=ax+bx+c(a≠0,a,b,c为常数),对称轴为直线x=1,它的部分自变量与函数值y的对应值如下表,写出方程ax2+bx+c=0的一个正数解的近似值________(精确到0.1).
| x | -0.1 | -0.2 | -0.3 | -0.4 |
| y=ax2+bx+c | -0.58 | -0.12 | 0.38 | 0.92 |
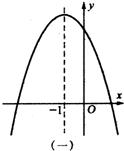 21、已知二次函数y=a(x+1)2+c的图象如图所示,则函数y=ax+c的图象只可能是( )
21、已知二次函数y=a(x+1)2+c的图象如图所示,则函数y=ax+c的图象只可能是( )
