题目内容
如图,抛物线y= x2通过平移得到抛物线m,抛物线m经过点B(6,0)和O(0,0),它的顶点为A,以O为圆心,OA为半径作圆,在第四象限内与抛物线y=
x2通过平移得到抛物线m,抛物线m经过点B(6,0)和O(0,0),它的顶点为A,以O为圆心,OA为半径作圆,在第四象限内与抛物线y= x2交于点C,连接AC,则图中阴影部分的面积为
x2交于点C,连接AC,则图中阴影部分的面积为 
 ﹣12.
﹣12.
解析试题分析:先求出抛物线m的解析式,得到顶点A的坐标,求出OA的长度,根据抛物线的对称性,可知阴影部分的面积=半圆的面积﹣△AOC的面积.
试题解析:∵抛物线m经过点B(6,0)和O(0,0),
∴抛物线m的对称轴为直线x=3,
∵抛物线y= x2通过平移得到抛物线m,
x2通过平移得到抛物线m,
∴设抛物线m的解析式为y= (x﹣3)2+k,
(x﹣3)2+k,
将O(0,0)代入,得 (0﹣3)2+k=0,
(0﹣3)2+k=0,
解得k=4,
∴抛物线m的解析式为y= (x﹣3)2+4,顶点A的坐标为(3,4),
(x﹣3)2+4,顶点A的坐标为(3,4),
由勾股定理,得OA=5.
连接OA、OC,由圆的对称性或垂径定理,可知C的坐标为(3,﹣4),
阴影部分的面积=半圆的面积﹣△AOC的面积= •π•52﹣
•π•52﹣ ×8×3=
×8×3= ﹣12.
﹣12.
考点: 二次函数图象与几何变换.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
 向上平移一个单位后,得到的抛物线的解析式是
向上平移一个单位后,得到的抛物线的解析式是 
 x+k=0有两个不相等的实数根,则k的取值范围是 _________ .
x+k=0有两个不相等的实数根,则k的取值范围是 _________ .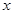 厘米,面积随之增加
厘米,面积随之增加 平方厘米,则
平方厘米,则 向左平移一个单位,所得抛物线的表达式为: .
向左平移一个单位,所得抛物线的表达式为: . +bx+c的图像如图所示,则不等式ax
+bx+c的图像如图所示,则不等式ax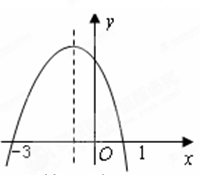

 ,
, 轴上有
轴上有 两点,以
两点,以 表示这两点间的距离,其中
表示这两点间的距离,其中 ,
, 的横坐标分别是方程组
的横坐标分别是方程组 的解,则
的解,则 的值等于 .
的值等于 .