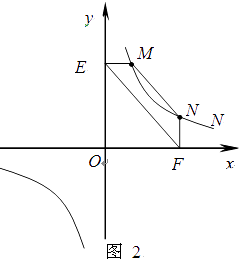��Ŀ����
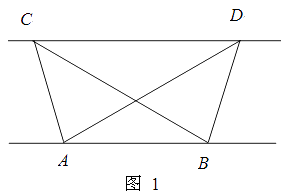
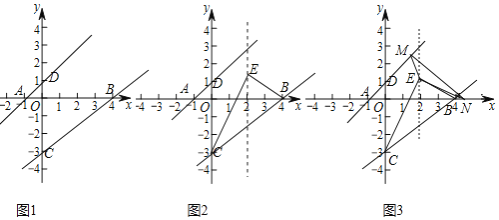
����Ŀ����ͼ1����Rt��ABC�У���A=90�㣬BC=10cm����P����Qͬʱ�ӵ�B��������P��2cm/s���ٶ���B��A��C�˶����յ�ΪC����Q��1cm/s���ٶ���B��C�˶�������P�����յ�ʱ������ͬʱֹͣ�˶������P��Q����t��ʱ����BPQ�����Ϊycm2 �� ��֪y��t�ĺ�����ϵ��ͼ����ͼ2������OM��MN��Ϊ�����ߵ�һ���֣����������½��ۣ���AC=6cm��������MN�Ľ���ʽΪy=�� ![]() t2+
t2+ ![]() t��4��t��7�������߶�PQ�ij��ȵ����ֵΪ
t��4��t��7�������߶�PQ�ij��ȵ����ֵΪ ![]() ��������PQC���ABC���ƣ���t=
��������PQC���ABC���ƣ���t= ![]() �룮������ȷ���ǣ� ��
�룮������ȷ���ǣ� ��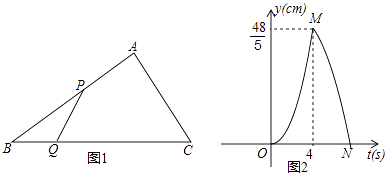
A.�٢ڢ�
B.�ڢۢ�
C.�٢ۢ�
D.�٢ڢ�
���𰸡�A
����������ͼ2�ɵõ�t=4ʱ��y= 48 5 ��
��AB=2��4=8cm��
�ߡ�A=90�㣬BC=10cm��
��AC=6cm��
�ʢ���ȷ��
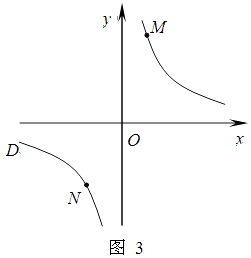
�ڵ�P��AC��ʱ����ͼ3����P��PD��BC��D��
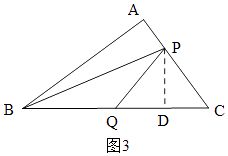
��ʱ�� ![]() =7��
=7��
��4��t��7��
������ã�AB+AP=2t��BQ=t��
��PC=14��2t��
sin��C= ![]() ��
��
�� ![]() =
= ![]() ��
��
��PD= ![]() ��
��
��y=S��BPQ= ![]() BQPD=
BQPD= ![]() t
t ![]() =��
=�� ![]() ��
��
�ʢ���ȷ��
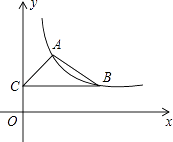
�۵�P��A�غ�ʱ��PQ�����ͼ4����ʱt=4��
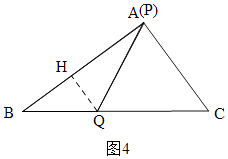
��BQ=4��
��Q��GH��AB��H��
sin�� ![]() ��
��
�� ![]() ��
��
��QH= ![]() ��
��
ͬ����BH= ![]() ��
��
��AH=8�� ![]() =
= ![]() ��
��
��PQ= ![]() =
= ![]() =
= ![]() ��
��
���߶�PQ�ij��ȵ����ֵΪ ![]() ��
��
�ʢ۲���ȷ��
������PQC���ABC���ƣ���Pֻ�����߶�AC�ϣ�
�����������
PC=14��2t��QC=10��t��
i������CPQ�ס�CBA����ͼ5���� ![]() ��
��
�� ![]() ��
��
���t=��8�������⣮
ii������PQC�ס�BACʱ����ͼ5��
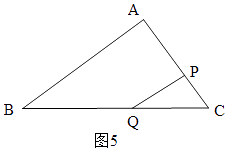
�� ![]() ��
��
�� ![]() ��
��
t= ![]() ��
��
������PQC���ABC���ƣ���t= ![]() �룬
�룬
�ʢ���ȷ��
������ȷ���У��٢ڢ�.
���Դ��ǣ�A��