Question

【题目】（问题引入）

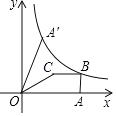
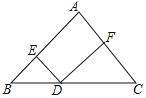
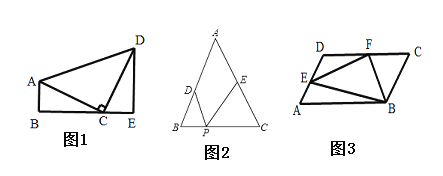
如图（1），在中，，，过作则交延长线于点，则易得

（直接应用）

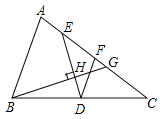
如图,已知等边的边长为,点, 分别在边, 上, , 为中点，为当上一动点，当在何处时，与相似，求的值.

（拓展应用）

已知在平行四边形中，，，，,，求长.

Answer 1

【答案】【直接应用】的值是或或；【拓展应用】

【解析】

(1)分两种情况进行假设：①和是对应边时,，或②和是对应边时,根据相似三角形的性质进行求解即可；

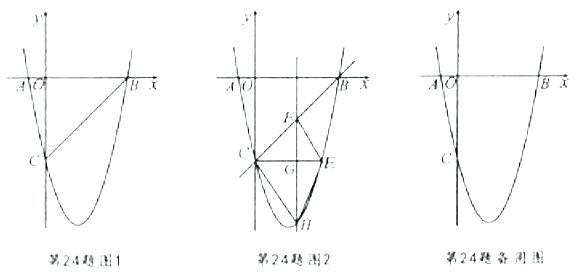
（2）反向延长EF，与BA，BC的延长线相交于点N、M，根据题意可得均为等腰三角形，从而求得，，将绕旋转到，作，可得，由勾股定理得再证明，即可得解.

[直接应用]

设

∵等边的边长为，

，

∵为中点，

，

①和是对应边时,，

，即，

整理得，解得，即的长为或；

②和是对应边时,，

，即，解得，即.

综上所述，的值是或或.

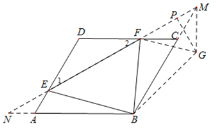
[拓展应用]

反向延长EF，与BA，BC的延长线相交于点N、M，

∵四边形ABCD是平行四边形，∠A=60°，AB∥CD,

∴∠D=120°，

∴∠ANE=∠CMF=30°, ∠AEN=∠CFM=30°

均为等腰三角形，

∵AE=2，CF=3，

易得，，

将绕旋转到，

，

作，

，

又

由旋转的性质得，BE=BG，∠ABE=∠GBC

∵∠A=60°

∴∠ABC=120°

∵∠EBF=60°，

∴∠ABE+∠CBF=60°，

∴∠GBF=60°=∠EBF，

又BF=BF

∴