Question

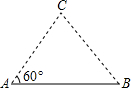两名滑冰运动员陈洁和李莉分别在平坦的冰面上的A点和B点如图，A点和B点之间的距离是100米，陈洁离开A以每秒8米的速度沿着与AB成60°角的直线上滑行，在陈洁离开A点的同时，李莉以每秒7米的速度也沿着一条直线滑行离开B点，这条直线能使这两名滑冰者以所给的速度最早相遇的时间是（　　）

• A、18秒
• B、20秒
• C、22秒
• D、

  100

  3

  秒

Answer 1

分析：设出相遇的时间，过点C作垂线，构造2个直角三角形，利用BC为斜边的直角三角形的三边可求得相应时间．

解答：解：过点C作CD⊥AB于D，设满足的时间为t，则AC=8t，BC=7t，
又∠A=60°，
∴AD=4t，CD=4

3

t，
∴根据勾股定理，得
（7t）²=（100-4t）²+（4

3

t）²，
解得t=20，或t=

100

3

（不合题意，舍去）．
故选B．

点评：本题考查解直角三角形在实际生活中的应用，构造特殊的直角三角形是常用的作辅助性方法．