题目内容
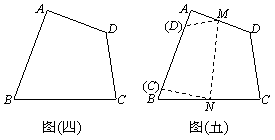
如图，在四边形ABCD中，AD∥BC，AM⊥BC，垂足为M，AN⊥DC，垂足为N，若∠BAD=∠BCD，AM=AN，求证：四边形ABCD是菱形．
证明：∵AD∥BC，
∴∠B+∠BAD=180°，∠D+∠C=180°，
∵∠BAD=∠BCD，
∴∠B=∠D，
∴四边形ABCD是平行四边形，
∵AM⊥BC，AN⊥DC，
∴∠AMB=∠AND=90°，
在△ABM和△ADN中，
，
∴△ABM≌△ADN（AAS），
∴AB=AD，
∴四边形ABCD是菱形．
练习册系列答案
相关题目
随着人民生活水平的提高，购买老年代步车的人越来越多．这些老年代步车却成为交通安全的一大隐患．针对这种现象，某校数学兴趣小组在《老年代步车现象的调查报告》中就“你认为对老年代步车最有效的管理措施”随机对某社区部分居民进行了问卷调查，其中调查问卷设置以下选项（只选一项）：
A：加强交通法规学习；
B：实行牌照管理；
C：加大交通违法处罚力度；
D：纳入机动车管理；
E：分时间分路段限行
调查数据的部分统计结果如下表：
| 管理措施 | 回答人数 | 百分比 |
| A | 25 | 5% |
| B | 100 | m |
| C | 75 | 15% |
| D | n | 35% |
| E |
| 25% |
| 合计 | a | 100% |
125（1）根据上述统计表中的数据可得m= ，n= ，a= ；
（2）在答题卡中，补全条形统计图；
（3）该社区有居民2600人，根据上述调查结果，请你估计选择“D：纳入机动车管理”的居民约有多少人？
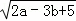+（2a+3b﹣13）2=0，则此等腰三角形的周长为（ ）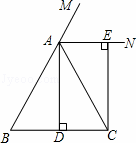
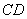迭合在
上，出现折线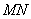
，再将纸片展开后，M、N 两点分别在
、
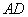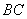上，如图(五)所示，则ÐMNB的度数为何？