Question

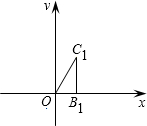已知：如图，在平面直角坐标系xoy中，点B₁、点C₁的坐标分别为（1，0），（1，

3

），将△OB₁C₁绕原点O逆时针旋转60°，再将其各边都扩大为原来的m倍，使OB₂=OC₁，得到△OB₂C₂．将△OB₂C₂绕原点O逆时针旋转60°，再将其各边都扩大为原来的m倍，使OB₃=OC₂，得到△OB₃C₃，如此下去，得到△OB₂₀₁₁C₂₀₁₁，则点C₂₀₁₁的坐标：

 

．

Answer 1

分析：可得旋转5次后，正好旋转一周，那么可得点C₂₀₁₁的坐标跟C₁的坐标在一条射线上，其横纵坐标均为原来的2010倍．

解答：解：∵每一次的旋转角是60°，
∴旋转5次后C在x轴正半轴上，
∴2011÷5=402…1，
∴点C₂₀₁₁的坐标跟C₁的坐标在一条射线上，
∵第2次旋转后，各边长是原来的2倍，第3次旋转后，各边长是原来的2²倍，
∴点C₂₀₁₁的横纵坐标均为原来的2010倍．
故答案为：（2²⁰¹⁰，2²⁰¹⁰

3

）．

点评：本题考查了坐标与图形变化-旋转及规律旋转后点的坐标，得到所求点的位置是解决本题的突破点；得到坐标的规律是解决本题的难点．