ÌâÄżÄÚÈĘ
ĄŸÌâÄżĄżÒŃÖȘĆŚÎïÏßy=aŁšx+3Ł©Łšx©1Ł©ŁšaĄÙ0Ł©ŁŹÓëxÖáŽÓŚóÖÁÓÒÒÀŽÎÏàœ»ÓÚAĄąBÁœ”㣏ÓëyÖáÏàœ»ÓÚ”ăCŁŹŸčę”ăA”ÄÖ±Ïßy=© ![]() x+bÓëĆŚÎïÏß”ÄÁíÒ»žöœ»”ăÎȘDŁź
x+bÓëĆŚÎïÏß”ÄÁíÒ»žöœ»”ăÎȘDŁź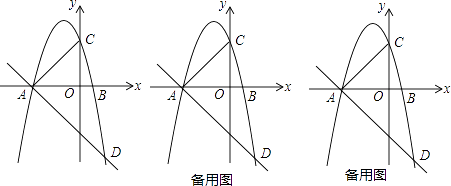
Łš1Ł©Èô”ăD”ÄșáŚű±êÎȘ2ŁŹÇóĆŚÎïÏß”ÄșŻÊęœâÎöÊœŁ»
Łš2Ł©ÈôÔÚ”ÚÈęÏóÏȚÄÚ”ÄĆŚÎïÏßÉÏÓĐ”ăPŁŹÊč”ĂÒÔAĄąBĄąPÎȘ¶„”ă”ÄÈęœÇĐÎÓ륜ABCÏàËÆŁŹÇó”ăP”ÄŚű±êŁ»
Łš3Ł©ÔÚŁš1Ł©”ÄÌőŒțÏÂŁŹÉè”ăEÊÇÏ߶ÎADÉÏ”ÄÒ»”㣚ȻșŹ¶Ë”㣩ŁŹÁŹœÓBEŁźÒ»¶Ż”ăQŽÓ”ăBłö·ąŁŹŃŰÏ߶ÎBEÒÔĂżĂë1žö”„λ”ÄËÙ¶ÈÔ˶Ż”œ”ăEŁŹÔÙŃŰÏ߶ÎEDÒÔĂżĂë ![]() žö”„λ”ÄËÙ¶ÈÔ˶Ż”œ”ăDșóÍŁÖ裏ÎÊ”±”ăE”ÄŚű±êÊǶàÉÙʱŁŹ”ăQÔÚŐûžöÔ˶ŻčęłÌÖĐËùÓĂʱŒäŚîÉÙŁż
žö”„λ”ÄËÙ¶ÈÔ˶Ż”œ”ăDșóÍŁÖ裏ÎÊ”±”ăE”ÄŚű±êÊǶàÉÙʱŁŹ”ăQÔÚŐûžöÔ˶ŻčęłÌÖĐËùÓĂʱŒäŚîÉÙŁż
ĄŸŽđ°žĄż
Łš1Ł©
œâŁșĄßy=aŁšx+3Ł©Łšx©1Ł©ŁŹ
Ąà”ăA”ÄŚű±êÎȘŁš©3ŁŹ0Ł©Ąą”ăBÁœ”ÄŚű±êÎȘŁš1ŁŹ0Ł©ŁŹ
ĄßÖ±Ïßy=© ![]() x+bŸčę”ăAŁŹ
x+bŸčę”ăAŁŹ
Ąàb=©3 ![]() ŁŹ
ŁŹ
Ąày=© ![]() x©3
x©3 ![]() ŁŹ
ŁŹ
”±x=2ʱŁŹy=©5 ![]() ŁŹ
ŁŹ
Ôò”ăD”ÄŚű±êÎȘŁš2ŁŹ©5 ![]() Ł©ŁŹ
Ł©ŁŹ
Ąß”ăDÔÚĆŚÎïÏßÉÏŁŹ
ĄàaŁš2+3Ł©Łš2©1Ł©=©5 ![]() ŁŹ
ŁŹ
œâ”ĂŁŹa=© ![]() ŁŹ
ŁŹ
ÔòĆŚÎïÏߔĜâÎöÊœÎȘy=© ![]() Łšx+3Ł©Łšx©1Ł©=©
Łšx+3Ł©Łšx©1Ł©=© ![]() x2©2
x2©2 ![]() x+3
x+3 ![]()
Łš2Ł©
œâŁș 
ŚśPHĄÍxÖáÓÚHŁŹ
Éè”ăP”ÄŚű±êÎȘŁšmŁŹnŁ©ŁŹ
”±ĄśBPAĄŚĄśABCʱŁŹĄÏBAC=ĄÏPBAŁŹ
ĄàtanĄÏBAC=tanĄÏPBAŁŹŒŽ ![]() ŁŹ
ŁŹ
Ąà ![]() ŁŹŒŽn=©aŁšm©1Ł©ŁŹ
ŁŹŒŽn=©aŁšm©1Ł©ŁŹ
Ąà ![]() ŁŹ
ŁŹ
œâ”ĂŁŹm1=©4ŁŹm2=1ŁšČ»șÏÌâÒ⣏ÉáÈ„Ł©ŁŹ
”±m=©4ʱŁŹn=5aŁŹ
ĄßĄśBPAĄŚĄśABCŁŹ
Ąà ![]() ŁŹŒŽAB2=ACPBŁŹ
ŁŹŒŽAB2=ACPBŁŹ
Ąà42= ![]()
![]() ŁŹ
ŁŹ
œâ”ĂŁŹa1= ![]() ŁšČ»șÏÌâÒ⣏ÉáÈ„Ł©ŁŹa2=©
ŁšČ»șÏÌâÒ⣏ÉáÈ„Ł©ŁŹa2=© ![]() ŁŹ
ŁŹ
Ôòn=5a=© ![]() ŁŹ
ŁŹ
Ąà”ăP”ÄŚű±êÎȘŁš©4ŁŹ© ![]() Ł©Ł»
Ł©Ł»
”±ĄśPBAĄŚĄśABCʱŁŹĄÏCBA=ĄÏPBAŁŹ
ĄàtanĄÏCBA=tanĄÏPBAŁŹŒŽ ![]() ŁŹ
ŁŹ
Ąà ![]() ŁŹŒŽn=©3aŁšm©1Ł©ŁŹ
ŁŹŒŽn=©3aŁšm©1Ł©ŁŹ
Ąà ![]() ŁŹ
ŁŹ
œâ”ĂŁŹm1=©6ŁŹm2=1ŁšČ»șÏÌâÒ⣏ÉáÈ„Ł©ŁŹ
”±m=©6ʱŁŹn=21aŁŹ
ĄßĄśPBAĄŚĄśABCŁŹ
Ąà ![]() ŁŹŒŽAB2=BCPBŁŹ
ŁŹŒŽAB2=BCPBŁŹ
Ąà42= ![]()
![]() ŁŹ
ŁŹ
œâ”ĂŁŹa1= ![]() ŁšČ»șÏÌâÒ⣏ÉáÈ„Ł©ŁŹa2=©
ŁšČ»șÏÌâÒ⣏ÉáÈ„Ł©ŁŹa2=© ![]() ŁŹ
ŁŹ
Ôò”ăP”ÄŚű±êÎȘŁš©6ŁŹ© ![]() Ł©ŁŹ
Ł©ŁŹ
ŚÛÉÏËùÊöŁŹ·ûșÏÌőŒț”Ä”ăP”ÄŚű±êÎȘŁš©4ŁŹ© ![]() Ł©șÍŁš©6ŁŹ©
Ł©șÍŁš©6ŁŹ© ![]() Ł©
Ł©
Łš3Ł©
œâŁș 
ŚśDMĄÎxÖáœ»ĆŚÎïÏßÓÚMŁŹŚśDNĄÍxÖáÓÚNŁŹŚśEFĄÍDMÓÚFŁŹ
ÔòtanĄÏDAN= ![]() =
= ![]() ŁŹ
ŁŹ
ĄàĄÏDAN=60ĄăŁŹ
ĄàĄÏEDF=60ĄăŁŹ
ĄàDE= ![]() EFŁŹ
EFŁŹ
ĄàQ”ÄÔ˶ŻÊ±Œät= ![]() =BE+EFŁŹ
=BE+EFŁŹ
Ąà”±BEșÍEFčČÏßʱŁŹtŚîĐĄŁŹ
ÔòBEĄÍDMŁŹy=©4 ![]() Łź
Łź
ĄŸœâÎöĄżŁš1Ł©žùŸĘ¶țŽÎșŻÊę”Äœ»”ăʜȷ¶š”ăAĄąB”ÄŚű±êŁŹÇółöÖ±ÏߔĜâÎöÊœŁŹÇółö”ăD”ÄŚű±êŁŹÇółöĆŚÎïÏߔĜâÎöÊœŁ»Łš2Ł©ŚśPHĄÍxÖáÓÚHŁŹÉè”ăP”ÄŚű±êÎȘŁšmŁŹnŁ©ŁŹ·ÖĄśBPAĄŚĄśABCșÍĄśPBAĄŚĄśABCŁŹžùŸĘÏàËÆÈęœÇĐΔÄĐÔÖÊŒÆËăŒŽżÉŁ»Łš3Ł©ŚśDMĄÎxÖáœ»ĆŚÎïÏßÓÚMŁŹŚśDNĄÍxÖáÓÚNŁŹŚśEFĄÍDMÓÚFŁŹžùŸĘŐęÇДĶšÒćÇółöQ”ÄÔ˶ŻÊ±Œät=BE+EFʱŁŹtŚîĐĄŒŽżÉŁź±ŸÌâżŒČé”ÄÊǶțŽÎșŻÊęÖȘʶ”ÄŚÛșÏÔËÓĂŁŹŐÆÎŐ¶țŽÎșŻÊę”ÄĐÔÖÊĄą¶țŽÎșŻÊę”Äœ»”ăÊœĄąÏàËÆÈęœÇĐΔÄĆжš¶šÀíșÍĐÔÖʶšÀíÊÇœâÌâ”ÄčŰŒüŁŹœâŽđʱŁŹŚąÒâ·ÖÇéżöÌÖÂÛËŒÏë”ÄÁé»îÔËÓĂŁź
ĄŸżŒ”ăŸ«ÎöĄżÍščęÁé»îÔËÓöțŽÎșŻÊę”ÄÍŒÏóșͶțŽÎșŻÊę”ÄĐÔÖÊŁŹŐÆÎŐ¶țŽÎșŻÊęÍŒÏńčŰŒü”ăŁș1ĄążȘżÚ·œÏò2Ąą¶ÔłÆÖá 3Ąą¶„”ă 4ĄąÓëxÖ᜻”ă 5ĄąÓëyÖ᜻”㣻ÔöŒőĐÔŁș”±a>0ʱŁŹ¶ÔłÆÖáŚó±ßŁŹyËæxÔöŽó¶űŒőĐĄŁ»¶ÔłÆÖáÓÒ±ßŁŹyËæxÔöŽó¶űÔöŽóŁ»”±a<0ʱŁŹ¶ÔłÆÖáŚó±ßŁŹyËæxÔöŽó¶űÔöŽóŁ»¶ÔłÆÖáÓÒ±ßŁŹyËæxÔöŽó¶űŒőĐĄŒŽżÉÒÔœâŽđŽËÌ⣟

ĄŸÌâÄżĄżÈçÍŒŁŹÒŃÖȘACĄÍBCŁŹBDĄÍADŁŹAC ÓëBD œ»ÓÚOŁŹAC=BDŁź
ÇóÖ€ŁșŁš1Ł©BC=ADŁ»
Łš2Ł©ĄśOABÊÇ”ÈŃüÈęœÇĐÎŁź

ĄŸÌâÄżĄżÎȘÁËŒÓÇż¶ÔĐŁÄÚÍâ°ČÈ«ŒàżŰŁŹŽŽœšÆœ°ČĐŁÔ°ŁŹÄłŃ§ĐŁŒÆ»źÔöŒÓ15ÌšŒàżŰÉăÏńÉ豞ŁŹÏÖÓĐŒŚĄąÒÒÁœÖÖĐÍșĆ”ÄÉ豞ŁŹÆäÖĐĂżÌšŒÛžńŁŹÓĐЧŒàżŰ°ëŸ¶Èç±íËùÊŸŁŹŸ”śČ飏čșÂò1ÌšŒŚĐÍÉ豞±ÈčșÂò1ÌšÒÒĐÍÉ豞¶à150ÔȘŁŹčșÂò2ÌšŒŚĐÍÉ豞±ÈčșÂò3ÌšÒÒĐÍÉ豞ÉÙ400ÔȘŁź
ŒŚĐÍ | ÒÒĐÍ | |
ŒÛžńŁšÔȘ/ÌšŁ© | a | b |
ÓĐЧ°ëŸ¶ŁšĂŚ/ÌšŁ© | 150 | 100 |
Łš1Ł©ÇóaĄąb”ÄÖ”Ł»
Łš2Ł©ÈôčșÂòžĂĆúÉ豞”ÄŚÊœđČ»łŹčę11000ÔȘŁŹÇÒÒȘÇóŒàżŰ°ëŸ¶žČžÇ·¶Î§Č»”ÍÓÚ1600ĂŚŁŹÁœÖÖĐÍșĆ”ÄÉ豞ŸùÒȘÖÁÉÙÂòһ̚ŁŹÇëÄăÎȘѧУÉèŒÆčșÂò·œ°žŁŹČąŒÆËăŚî”ÍčșÂò·ŃÓĂŁź
ĄŸÌâÄżĄż10ÔÂ21ÈŐŁŹĄ°ÖĐčúÁś¶ŻżÆŒŒčĘĄ±ŃČŐčÆô¶ŻÒÇÊœÔÚĐ»ȘÇűÇàÉÙÄê»î¶ŻÖĐĐÄÊąŽóŸÙĐĐŁŹŽËŽÎŃČŐčÒÔĄ°ÌćŃéżÆѧĄ±ÎȘÖśÌ⣟žĂÇűÄłÖĐѧŸÙĐĐÁËĄ°żÆÆŐÖȘʶĄ±ŸșÈüŁŹÎȘÁËœâŽËŽÎĄ°żÆÆŐÖȘʶĄ±ŸșÈüłÉŒš”ÄÇéżöŁŹËæ»úłéÈĄÁËČż·ÖČÎÈüѧÉú”ÄłÉŒšŁŹŐûÀíČąÖÆŚśłöÈçÏ”ÄČ»ÍêŐû”ÄÍłŒÆ±íșÍÍłŒÆÍŒŁŹÈçÍŒËùÊŸŁźÇëžùŸĘÍŒ±íĐĆÏąœâŽđÒÔÏÂÎÊÌ⣟
Śé±đ | łÉŒš | Æ”Êę |
AŚé |
|
|
BŚé |
| 12 |
CŚé |
| 18 |
DŚé |
| 21 |
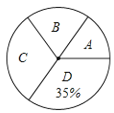
Łš1Ł©±íÖĐÒ»čČłéÈĄÁË________žöČÎÈüѧÉú”ÄłÉŒšŁ»![]() ________Ł»
________Ł»
Łš2Ł©ÇółöŒÆËăÉÈĐÎÍłŒÆÍŒÖĐĄ°![]() Ą±”ÄÔČĐĜǶÈÊ꣟
Ą±”ÄÔČĐĜǶÈÊ꣟
Łš3Ł©ÈôłÉŒšÔÚ90·ÖÒÔÉÏŁš°üÀš90·ÖŁ©”ÄÎȘĄ°ÓĆĄ±”ÈŁŹÒŃÖȘžĂĐŁčČÓĐ1200ĂûѧÉúŁŹÇëÄăčÀŒÆžĂĐŁÔŒÓжàÉÙĂûѧÉú”ÄłÉŒšÊÇĄ°ÓĆĄ±”ÈŁź




