题目内容
如图,直角坐标系中Rt△ABO,其顶点为A(0, 1)、B(2, 0)、O(0, 0),将此三角板绕原点O逆时针旋转90°,得到Rt△A′B′O.

(1)一抛物线经过点A′、B′、B,求该抛物线的解析式;
(2)设点P是在第一象限内抛物线上的一动点,是否存在点P,使四边形PB′A′B的面积是△A′B′O面积4倍?若存在,请求出P的坐标;若不存在,请说明理由.
(3)在(2)的条件下,试指出四边形PB′A′B是哪种形状的四边形?并写出四边形PB′A′B的两条性质.
(1)y=-x2+x+2;(2)P(1,2);(4)四边形PB′A′B为等腰梯形,答案不唯一,①等腰梯形同一底上的两个内角相等;②等腰梯形对角线相等.
【解析】
试题分析:(1)利用旋转的性质得出A′(-1,0),B′(0,2),再利用待定系数法求二次函数解析式即可;
(2)利用S四边形PB′A′B=S△B′OA′+S△PB′O+S△POB,再假设四边形PB′A′B的面积是△A′B′O面积的4倍,得出一元二次方程,得出P点坐标即可;
(3)利用P点坐标以及B点坐标即可得出四边形PB′A′B为等腰梯形,利用等腰梯形性质得出答案即可.
试题解析:(1)(1)△A′B′O是由△ABO绕原点O逆时针旋转90°得到的,
又A(0,1),B(2,0),O(0,0),
∴A′(-1,0),B′(0,2)
设抛物线的解析式为:y=ax2+bx+c(a≠0),
∵抛物线经过点A′、B′、B,
∴ ,解得:
,解得: ,
,
∴满足条件的抛物线的解析式为y=-x2+x+2.
(2)∵P为第一象限内抛物线上的一动点,
设P(x,y),则x>0,y>0,P点坐标满足y=-x2+x+2.
连接PB,PO,PB′,

∴S四边形PB′A′B=S△B′OA′+S△PB′O+S△POB,= ×1×2+
×1×2+ ×2×x+
×2×x+ ×2×y=x+(-x2+x+2)+1=-x2+2x+3.
×2×y=x+(-x2+x+2)+1=-x2+2x+3.
∵A′O=1,B′O=2,∴△A′B′O面积为: ×1×2=1,
×1×2=1,
假设四边形PB′A′B的面积是△A′B′O面积的4倍,则
4=-x2+2x+3,
即x2-2x+1=0,
解得:x1=x2=1,
此时y=-12+1+2=2,即P(1,2).
∴存在点P(1,2),使四边形PB′A′B的面积是△A′B′O面积的4倍.
(3)四边形PB′A′B为等腰梯形,答案不唯一,①等腰梯形同一底上的两个内角相等;②等腰梯形对角线相等;③等腰梯形上底与下底平行;④等腰梯形两腰相等.
考点: 二次函数综合题.

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案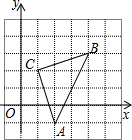 如图,直角坐标系中,△ABC的顶点都在网格点上,其中,A点坐标为(2,-1),则△ABC的面积为
如图,直角坐标系中,△ABC的顶点都在网格点上,其中,A点坐标为(2,-1),则△ABC的面积为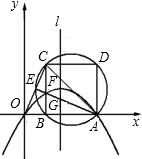 ?若存在,请求出所有这样的点;若不存在,请说明理由.
?若存在,请求出所有这样的点;若不存在,请说明理由. 在如图平面直角坐标系中,△ABC三个顶点A、B、C的坐标分别为A(2,-1),B(1,-3),C(4,-4),
在如图平面直角坐标系中,△ABC三个顶点A、B、C的坐标分别为A(2,-1),B(1,-3),C(4,-4), 如图,直角坐标系中,△ABC的顶点都在网格点上,C点坐标为(1,2),原来△ABC各个顶点纵坐标不变,横坐标都增加2,所得的三角形面积是
如图,直角坐标系中,△ABC的顶点都在网格点上,C点坐标为(1,2),原来△ABC各个顶点纵坐标不变,横坐标都增加2,所得的三角形面积是 在如图的直角坐标系中,将△ABC平移后得到△A′B′C′,它们的个顶点坐标如表所示:
在如图的直角坐标系中,将△ABC平移后得到△A′B′C′,它们的个顶点坐标如表所示: